CRYPTO:
The Alchemy of Diplomacy
by Kevin Burt
|
Crypto encompasses cryptography (hidden or secret writing), cryptology and cryptanalysis.
A popular dictionary defines alchemy as “a seemingly magical process of transformation, creation, or combination”. So it is with crypto, the making (and breaking?) of codes and ciphers.
A National Security Agency (NSA) report I referenced in the accompanying article The Zimmermann Telegram (DPZine, S2016M) declares “deciphering the Zimmerman telegram was the greatest cryptologic triumph [later called a coup] of the First World War.”
Dare I disagree with the NSA?
The Zimmermann telegram was coded, and not encrypted rendering it a cipher. Breaking cipher is an accomplishment — a triumph, a coup.
Codes operate by substituting words and phrases according to a codebook, often large and ponderous.
The telegram was broken by cryptanalysts reading a captured book, and what is termed “brute force” — or trial and error. In this instance, the British had a captured German codebook. It certainly did not contain every conceivable word — but it contained the words the intended recipient would have in his code book. The British had annotated their captured book with handwritten words they had added as they were brute-forcibly decoded earlier.

The image above is a WWII German codebook. It is small and concise, so I’d think it was for a battalion regimental radio network. The code zrk, incidentally, decodes to zurückziehen or zurückgehend for retreat or withdraw. The Zimmermann note used numerals as coded word groups.
We have all seen word jumbles or “Cryptograms” published in newspaper intended for entertainment. It’s my opinion decoding the Zimmermann telegram was really no more difficult, and perhaps, less so.
Mixed like a salad
One of the oldest and, frankly, least difficult is the Caesar Cipher. Caesar reportedly devised and used it. It operates on the alphabet, and the “key” is a monoalphabetic charter-shift. A three-character shift would cipher A as D; B becomes E; and so on. To decrypt, D becomes A . . .
If the Gaul captured (intercepted) the message, the courier (if he was alive and literate) could easily decrypt it.
The Confederate (States of America) Secret Service movable “disk” (pictured below) is depicted with a 17-character shift. The plaintext letter (inner disk) A => R in the photo. T is K, and so forth. [Ed: I had a Secret Squadron decoder badge and Capt. Midnight sent me a message every Saturday morning.]
 |
You can decrypt DVVK DV RK RGGFDRKKFO.
If it is transmitted as DVV KDV RKR GGF DRK KFO, or DVVKD VRKRG GFDRK KFO some small difficulty is added. It helps to “see” encrypted the word, the letter pattern.
In a short message this might be of help DVVKDVRKRGGFDRKKFO.
General Alice and General Bob (crypto conventions) might to set the plaintext to the outer circle the following day. The disks could be (or should have been) “scrambled” (set to another shift or key) periodically.
The cryptanalysis begins. The cryptanalyst might begin his efforts looking for double letters (in the ciphertext) that could decrypt to EE, MM, OO, PP, TT and so on. My examples aren’t exhaustive.
The analyst looks for ciphertext letter frequency. The letter E is the most common letter used in many languages (13% in English) – followed by T and O. The cryptanalyst also examines the message in context used, for this contains many (unintentional) clues. Here’s some others, gimmes: it was intercepted in Northern Virginia in 1865.
In our example problem, the repeated V and it’s position in another word allow for easy and quick decryption. Right . . ?
Focus on these two words DVVKDV (another clue) . . . These mental gymnastics are the application of “brute force”.
Ciphers have progressed through time and difficulty. Simple ciphers were used and then encrypted with a more difficult cipher. They progress as I write and you (I hope) read this.
The next significant step was the polyalphabetic Vigenère Cipher and navigating the tabula recta.

The tabula recta
Vigenère called his method le chiffre indéchiffrable — the indecipherable cipher.
The six-letter term DPZINE is determined as today’s “key”. To begin we read down the first column to D (first letter of our key). We read across that row to P (the second letter). Reading up to the topmost row is M.
We might use that simple example to test the recipients’ bona fides. Our challenge is "Delta Papa" (D and P phonetically); their response should be "Mike" (M). [Ed. note: I was in the field artillery, and that is, in fact, how we opened the radio network (net) at the beginning of the day in the field. Failure to reply with the valid response on two or three attempts, and, as is said, the proverbial substance flowed down hill. That's my last 'war story'.]
|
LEFTMOST COLUMN
|
D
|
P
|
Z
|
I
|
N
|
E
|
D
|
P
|
Z
|
I
|
N
|
E
|
|
READ ACROSS ROW TO
|
A
|
T
|
T
|
A
|
C
|
K
|
A
|
T
|
D
|
A
|
W
|
N
|
|
READ UP TO TOP ROW:
|
D
|
I
|
S
|
I
|
P
|
O
|
D
|
I
|
C
|
I
|
J
|
R
|
We want to encrypt General Alice’s instructions “Attack at dawn” to General Bob. Enemy forces, under the command or General Eve (another crypto convention for "eavesdropper", or "enemy") are in the area.
We take the letter we will be encoding, 'A', and find it on the first column on the table. Then, we move along the 'A' row of the table until we come to the column with the 'D' at the top (The 'D' is the first letter for the first 'DPZINE'), the intersection is our ciphertext character, 'D'.
Our example is immediately unique. The first encrypt on the A row (the second row) is somewhat unfortunate (the ciphertext is the same as the plaintext) but it is only one letter. Or, is replacing the plaintext with the same ciphertext in fact a fortuitous event? It is just one letter. The cryptanalyst’s paradigm is to look for one letter decrypting to another, and this might delay her.
And examine the number of Is (letter eye). They are misleading, as they do not encrypt to E (normally the most frequent letter), and are distributed in our encrypted message.
To decrypt the message at the receivers end. We know the key: DPZINE. We have the encrypted message in our trembling hands.
|
KEY
|
D
|
P
|
Z
|
I
|
N
|
E
|
D
|
P
|
Z
|
I
|
N
|
E
|
|
ENCRYPT
|
D
|
I
|
S
|
I
|
P
|
O
|
D
|
I
|
C
|
I
|
J
|
R
|
| DECRYPT |
A |
T
|
T
|
A
|
C
|
K
|
A
|
T
|
D
|
A
|
W
|
N
|
The technique to decrypt is a logical walk backwards from how the plaintext was encrypted. Keep in mind the key: DPZINE.
|
Read down the leftmost column to D;
Read across the row to the
encrypted letter D;
Read up to the topmost row: A!
|
Read down the leftmost column to P;
Read across to the row to the encrypted letter I;
Read up to the topmost row: T!
|
Read down the leftmost column to Z;
Read across the row to the encrypted letter S;
Read up to the topmost row: T!?
|
Wait! How could T be decrypted from both an I and an S? Because it is polyalphabetic cipher. Using the key and the plaintext, the ciphertext is likely to produce different letters.
The inventor of this code claimed it was “unbreakable”. It was for a long time, and then came mechanization and electronics.
The Enigma machine
The Enigma machine was invented for practical business purposes. The German Wehrmacht saw its military uses.
We have used a simple “key” above (DPZINE). The Enigma machine encrypted the plaintext multiple (hence polyalphabetic) times. Every time a 27th character was typed the key changed. The resulting permutations that, alone, make decryption almost, almost impossible or at least untimely.
Let’s look over an operators shoulder.
All settings were predetermined and universal throughout a particular branch, the Wehrmacht, Luftwaffe, and Kriegsmarine.
The operator arranges a plugboard (similar a vintage telephone switchboard). It can be arranged and wired to 13 combinations via two-ended plugs: (e.g. A is plugged with X, etc.).
Looking at the plugboard we have 26 letters arrayed in the manner of the keyboard. When I select the first letter, I have 25 choices for the second. The second combination setting allows me 24 choices for the first, two letters (A and X) are already plugged and unavailable, and 23 for the second letter.
Is it not, then:
26x25 + 24x23 + 22x21 + 20x19 + 18x17 + 16x15 + 14x13 + 12x11 + 10x9 + 8x7 + 6x5 + 4x3 + 2x1
Depending on the Enigma model, from three to seven rotors are selected. The rotors are then preset to alphabetic keys. TDP, ADOLF, SEALION, whatever . . .

The Enigma plugboard
The process is repeated for another 13 pairings for the returning current turned into an enigma.
Just based on what I have described so far (there was probably more to set-up the device) I calculate 26 alphabetic settings for one rotor. (Numerals were spelled out. That seems quite unsophisticated for this devilish device). Multiply that by the number of rotors (3 through 7) times the number of possible rotor internal wiring settings, or 263 or 17, 576 possible settings in one direction of the current. The plugboard selections gave us an initial possibilities of (i.e. 26 x 25 + 24 x 23 + 22 x 21… Beginning, I chose one letter; I plug the other end into one of only 25 possibilities. The second plug wire gives me 24 x 23 possibilities. And again.
As I type A, the three rotors’ internal wiring click 26 x 26 x 26 possible changes.
For example, say A: becomes M at the first rotor, M becomes T at the second rotor, and T becomes N at the third rotor. N is returned through the three rotors to the key board and the wiring combination it is assigned is N to B. The B lights up on the keyboard.
 Enigma’s keyboard and rotors
Enigma’s keyboard and rotors
On the twenty-sixth keyboard strike, the second rotor clicks over and a “new” rotor combination is “online” scrambling the next letter typed. Think of an analog odometer: After the ninth mile, at the tenth, the first and second rotors read 9 and 0 [09] respectively and become 10. After that on the 52nd keyboard strike, the third rotor “clicks” (along with the second and first) over and our “mileage” now reads 100.
In a lengthy message (the Zimmermann note was 1,000 word groups) you’re continually applying new cipher to the remainder of the message.
And, again, the character returned passes through the wiring sets. The second character typed lights the K etc, etc, etc.
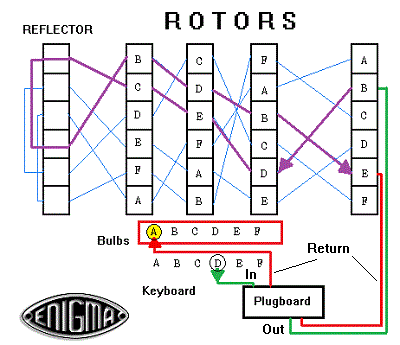 A diagram of electric current “flow chart” for afive-letteralphabet, four rotors, and a reflector.
A diagram of electric current “flow chart” for afive-letteralphabet, four rotors, and a reflector.
Decrypting must rely on patterns for solution. The Enigma obliterates pattern with each and every stroke. I can’t do the math – the possibilities for one keystroke is more than 46 million after transgressing the rotors and 2 billion after the wiring switchboard. Then comes the second character . . .
So how was Enigma then “broken”? It was a combination of brute force, two “flaws”, and a bombe.
The brute force was exerted by thousands of workers visually and audibly reading what they could of German transmissions. They tried to tie past events (some immediate) and they knew about to the encrypted text generated at that time locations (is the speaker voice ‘recognized’? Telegraphers can be ‘recognized’. Do we know his location?). Example: A weather report is generated every day. We can decrypt the various parameters – wind speed, and direction; general conditions (cloudy), temperature 17c. Those small bits information begin to add up, becoming “bites”. Communications probably would consistently sign off with HEIL HITLER. The idea is to glean as much information possible, decrypt what we can before the rotor clicks on the 27th letter. Then the process begins again.
Presume we have decrypted the weather report. Suppose a ship at sea asks for a repeat of the weather report? If the rotor has clicked-over, now we have the same parameters sent in the new encrypt. We can decrypt a little more.
If we have a grasp of how the letter H is encoded, from the weather report signed off with HEIL HITLER, might we have a “leg up” on message traffic regarding some activity in the Helgoland Bight HELGOLAND BIGHT? What, in addition, have we decrypted from the mundane weather report? “Brute force” is not as inelegant as the word implies.
The two flaws of Enigma were first that it would not repeat the same letter (e.g.OO (oh oh) might read DM, but not DD, nor MM). That deleted one possible character from the encrypted text. Secondly it did not repeat itself. If one typed A, another A would never be displayed for the same typed letter. It may seem insignificant, but it meant something. In codebreaking, you often find the code by excluding impossibilities. The de-cryptanalyst now know something about the ciphered text!
The bombe was the name the codebreakers gave a computer developed by cipher-breakers at Bletchley Park during WWII.
Today’s riddle, wrapped in a mystery, inside an enigma*
We are touched by ciphers and cryptography throughout the day. If you glance up and look at the url address bar, does it have a small green lock? If so, you are secure.
As you’ve seen, the alchemy of crypto depends on mathematics.
I’ll show a very, very, very simple example, and progress just a bit.
Much of what you do online is encrypted. You are using encryption at the ATM machine, gas station pump. Be multiplied by a key -- shared between you and the business or email recipient.
An overly simplified partial explanation: Your key is 187.
If our cryptography was only as advanced as to ask your two favorite numbers (mine are 11 and 17) and multiple them for the product of 187 we would be hacked pretty quickly. To verify the key, I have to divide by 11 or 17 to get a whole number. Trial-and-error wouldn’t even take long. Maybe much of it has been done in advance, and 187 is immediately recognized.
It is used in a calculation (algorithm is the highfalutin term) with your credit card number and your personal identification number (pin). When the merchant begins to fulfill the transaction, the answer to the algorithm must be evenly divisible by 187, and in turn 187 is only whole numbers that can be evenly divided by 11, 17 with a whole number result. Of course 187 is evenly divided by itself, but that algoritm excludes 1.
In reality your key is a number that would rival an Enigma probability in size and value: Hundreds, if not thousands of numerals in different-base numbering systems. No trial-and-error method could work in a lifetime.
There is no dearth of information on crypto on the Internet, and in books.
And there you have it. I appreciate your patience.
Kevin is retired and lives in Florida, or La Florida as the 16th century Spanish Conquistadores named it. He is recovering from a mental breakdown suffered upon completing this article. He assists with editing The Zine.
If you wish to e-mail feedback on this article to the author, and clicking on the envelope above does not work for you, feel free to use the "Dear DP..." mail interface.