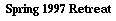

Note from the author: This paper does not provide the promised sequel to my first article. That is it will not cover non-game theoretical approaches in IR (such as Robert Jervis' Theory of Misperception). It will instead be just another game theoretical paper. But it is in my opinion far better than the first. That early assay into unknown waters displayed some interesting failures to grasp basic concepts. Informed by a year of hard-core Rational Choice courses, this one should promise more.
The objective of the game, and its condition of systemic anarchy (there is no higher power than the players beyond the technical rules of the game) provide a Hobbseian condition undoubtedly purer than the international reality deduced by the harshest of neorealist theorists 5. Moreover, the lack of the status quo as a preferred final outcome for any player (as opposed to in the real world) 6 coupled with a normative environment that typically admires guile, deviousness and ruthlessness, drastically limits the power of moral constraints in mitigating the state of nature. Keeping in mind that as in all zero-sum games, others' gains and losses effect the relative position of each player, the simplifying assumption of egoism requires little justification in Diplomacy.
The two fundamental underpinning assumptions of Rational Choice are methodological individualism and purposeful action 7. Methodological individualism simply means that outcomes can be understood by reference to individual preferences and choices, rather than through institutional characteristics or collective units of analysis. To analyze real political events with Rational Choice Theory, making this assumption necessitates coming down firmly on one side of a great methodological debate; to so analyze Diplomacy, no such commitment is necessary. Players are individuals, and though decisions as to which orders to give may be influenced by other players, the institution that provides the basic level of input which leads to outcomes on the "macro" scale of the game is the player. The analyst will find no barrier here to further examination of Diplomacy.
Purposive action is simply the assumption of rationality itself. Actions are aimed at achieving outcomes, and all outcomes have transitive preference relationships to each other. A rational player will always choose those actions that he believes will lead to the outcome that he most prefers, of those possible. Diplomacy players on the whole (there are always exceptions of course) would seem to offer little difficulty to the rationality assumption, assuming reasonably that they have read the rules well enough to understand which actions lead to which outcomes.
However, there may be a problem with transitivity when applied to the expectations of a player in assuming the motivations of other players. Given that each player knows the other players' preference rankings and has a preference ranking which is known to all other players (and that each player knows that the others know that player's preference rankings, and so on) - possible outcomes and payoffs are common knowledge - a Game Theoretical analysis is possible. While all rational players should have transitive preferences, problems arise if one or more players have non-standard preference rankings (i.e., other those stipulated by the rules). Though a player with non-standard preference rankings will still likely conform to the rationality assumption necessary for Rational Choice analysis (the non-standard preferences may still be transitive, and the players actions will still aim to achieve the best possible outcomes as he sees them), the effect will hinder the attempts of other players and of the analyst to analyze the behavior of the player. The standard preferences are as follows:
Even if this player declares his true preferences, the others will assume, as well they might, that the true carebear is just another "cutthroat" like themselves. Thus although a player with non-standard preference rankings will not be irrational from his own perspective, the nature of the game will confound the attempts of other players - and the analyst - to predict his behavior. The practical effect is the same as if the player was actually irrational as that player's actions will not be aimed at achieved at aiming what others' expect to be his most preferred outcome - winning. Of course, it might be possible for players to incorporate the probability that other players have non-standard preferences into their considerations. But this, while not making analysis impossible, makes it extremely complex. For the purposes of this paper, the models given assume that all players have standard preference rankings 8.
Another requirement of standard Game Theory is that preferences remain fixed throughout the game. While the actions of others interacting with the actions of the player must effect the outcome for Game Theory to be applicable 9, actions of other players should not effect the preferences of the player. Game Theoretical analysis will be distorted if a particular player's preferences change in the course of game due to the actions of others. This typically happens when a player holds a grudge, or suffers from "sour grapes" syndrome. For example, if player A attacks player B, and player B's preference rankings change so that B prefers elimination to surviving if this survival involves Player A's victory (or even survival), the analyst is stymied.
Again, there is some incentive for every player to give the impression that his preferences will change in just this way, to make threats credible in the common cases where carrying out threat will lead to the threatener's elimination. Thus the presence of a grudge-holding player - given that true preferences at variance with the standard preferences are unlikely to be believed - frustrates rational analysis in the same way that does the presence of a player with constant but non-standard preferences. And again, the models here assume players with constant preference rankings.
However, though Diplomacy is in fact a zero-sum game, it is not a 2-person zero-sum game (unless all other players but two have been eliminated). This significantly limits the predictive power of the analyst, and of the players. All 2-person zero-sum games have equilibria in pure or mixed strategies. Moreover, all equilibria are equivalent and interchangeable 10. This does not hold for n-person zero-sum games 11. First, many equilibria may exist for which the results of each are not equivalent to the other. Second, the particular strategies that lead to a given equilibria will not be the same as those that lead to another. Since players have no way of determining which equilibria will be reached, they have no way of knowing which strategies will lead to an equilibria, and will in most cases have no way of determining with certainty which strategy would maximize their utility given the strategies of the other players. Thus, while describing Diplomacy as an n-person zero-sum game is accurate, this offers little more than the possibility of making broad generalizations of little use to players or analysts wishing to make predictions.
Rather than end the discussion on this note of futility, it may be possible to move forward with Game Theoretical analysis by making an assumption. This is that the whole of game Diplomacy can be usefully broken down into a set of sub-games that in themselves differ from the characteristics of n-person zero-sum games. In the interactions between subgroups of players, strategizing may be functionalized by reference to other sorts of games - 2-person zero-sum, 2- and n-person games of conflict and cooperation, even 2-person and n-person games of coordination. All manner of games be taking place simultaneously, bearing in mind that they all fit together under and are constrained by the overall n-person zero sum game.
In Diplomacy, outright conflicts with other players have the aspect of 2-person zero-sum games. The efforts of two wary players to form a new alliance often follow the pattern of iterated cooperative games, where reciprocity - or outside threat - may succeed in building trust to the point where two allies can coordinate their moves in order to make the best use of all their units. For example, Turkey might consider his dealings with an attacking and uncommunicative Russia as a two-person zero-sum game, while attempting to overcome Prisoner's Dilemma logic in establishing an alliance with Austria. Meanwhile England - facing elimination - might feel the need to coordinate perfectly his moves with Germany and Italy against an ascendant France. And yet the overall structure of the n-person zero sum game holds dynamics which often lead to players reconsidering which sub-games they are playing in reference to the overall situation. So Turkey may pause in his successful campaign to gain at Russia's expense if this will lead to Austria's victory, and England, once secure, might change from coordinating moves with Germany to plotting against him, once the threat from France has been beaten back, and Italy may re-frame his understanding of cooperative agreement with Austria after the Kaiser's armies begin pouring over the border into a 2-person zero-sum game of minimizing losses.
What makes a good player, or a good analyst, of Diplomacy is the ability to ascertain which sub-games are appropriate for understanding and thus strategizing in a given game situation. To act as if you are in a game of coordination with a neighbor when in fact he is thinking in zero-sum terms, with your losses being his gains, is to invite disaster. Conversely, failing to see that another player is about to achieve victory might cause one to continue falling into the trap of Prisoner's Dilemma logic with those with whom the best and most urgent strategy would call for coordination.
The appropriate games to be played are a function of expected benefits of strategies, given which games other players are thought to be playing for that game turn. In certain situations, such as when one player is about to win the game, the sub-games are clear, and players tend to coordinate against the pretender, while the would-be victor attempts to maximize his chances of victory utilizing mixed and pure strategies within the context a 2-person zero-sum game of him against a grand coalition. The pretender often holds an advantage aside from any positional details in that he need only coordinate his side of the zero-sum within his head, while those that would prevent his victory must play a game of coordination with each other at the same time as they as a group must face the pretender. On the other hand, a group, given the inherent limitations in analyzing often immensely complicated possibilities, may hold an advantage in that many minds may find solutions that one may miss, especially under time constraints that exacerbate bounded rationality.
| Orders: | Italian Army in Piedmont | ||
|---|---|---|---|
| To Mar | Holds | ||
| French Army in Spain | to Mar | 0 | -2 |
| Hold | -5 | 0 | |
If France holds to a pure strategy maximin strategy and simply orders back to Marseilles, and Italy expects this, Italy can simply hold to guarantee a payoff of 2. Yet France will not profit by simply flipping a coin: if Italy perceives this strategy, he will surely order to Marseilles as the expected payoff is 2.5 [1/2(-5)+1/2(0)], even higher than if France had followed a pure-strategy maximin strategy. Yet the simplicity of 2-person zero-sum games with only two options for each player allows for the best strategy to be determined algebraically (more complicated situations can be solved with calculus). From France's point of view, his losses are minimized if he moves to Marseilles with a probability of P, and probability P is maximized in respect to Italy's possible options.

| 0P -2(1-P) | = | -5P+0(1-P) |
|---|---|---|
| P | = | 5/7 |
This strategy yields an expected value to France of -10/7, no matter what strategy Italy follows. However, Italy is, faced with this logic, is best advised to move to Marseilles 2/7 of the time (the game is symmetrical), for if France anticipates that Italy will choose another strategy, France will have incentive to change to a pure strategy. For example, if Italy decides to move to Marseilles 1/2 the time, France can achieve an expected payoff of -1 if he moves to Marseilles with a probability of 1 [1/2(0)+1/2(-2)].
Although the previous model may be of use to players in maximizing their gains in uncertain situations (of which Diplomacy is full), the model is not very interesting for the analyst. It would be much more interesting to derive a model that went some way toward understand the basic flow of Diplomacy from opportunistic alliance to back-stabbing to last-ditch efforts at coordinating against a would-be winner. To do so in anything near a complete manner would take more paper than exists, as the possible permutations involved in just one Diplomacy move stretch into the trillions. Something in between the simple model that explains little more than a tactical technique and a complete one that explores the full strategic dynamics of the game is therefore needed. By limiting the players to three (which occurs if four players are eliminated, as well as with some Diplomacy variants) 12, and the action sets to strategic decisions, even limiting these to less that than the conceivable at four, a model is presented that, while only scratching the surface of the games' logic, may illuminate.
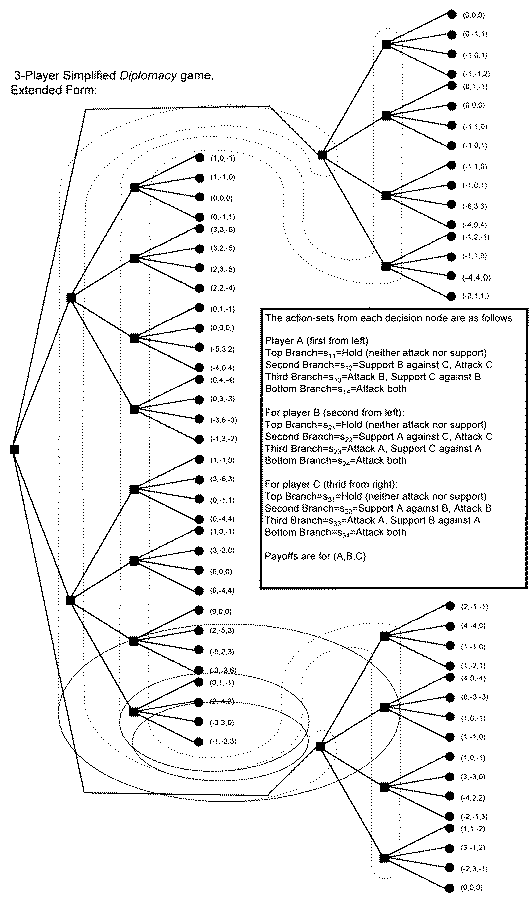
Consider a game of Diplomacy between players A, B, and C, each controlling powers in symmetrical positions. The following strategies for player A against players B and C to be played simultaneously:
s11=Hold (attack nor support neither opponent)
s12=Support B against C, Attack C
s13=Attack B, Support C against B
s14=Attack both
For player B:
s21=Hold (attack nor support neither opponent)
s22=Support A against C, Attack C
s23=Attack A, Support C against A
s24=Attack both
For player C:
s31=Hold (attack nor support neither opponent)
s32=Support A against B, Attack B
s33=Attack A, Support B against A
s34=Attack both
The expected values of attacking are in an arbitrary but ranked relatively scaled point system as follows:
As the game is zero-sum, gains by the attacker are equal to losses by the player attacked. For example, with the strategy set {s13, s22, s34} the result for A is 0 (1 for attack against B -1 from attack by C), for B is -3 (-1 from attack by A, 0 from attack on C, -2 from the supported attack by C), and the payoff for C is 3 (1 from the attack on A, 2 from the supported attack on C).
With even this limited set of strategies, there are 64 possible outcomes. This is barely manageable in extended form (see picture below). An analysis of the game tree provides some insights into the basic logic of a Diplomacy turn. At any point on the tree, the dominant strategy for each player is to attack both of the others. As the game is symmetrical, this results in an equilibrium strategy set of {s14, s24, s34} yielding a payoff to each player of 0. Yet this is not a better outcome than what can be achieved by two players working in concert against the third. For example {s12, s22, s34} yields a payoff of 2,2, and -4 for A, B, and C respectively. However, any attempt to cooperate is hindered by fears that the other player will take advantage of the support to make an even larger gain. If player B plays s24 instead of s22 the payoffs will change to 0, 3, -3, and of course player B rationally prefers 3 to 2. The temptation to defect exists for all would-be coalition partners. It is not possible to overcome this Prisoner's dilemma logic in a one-shot, or rather a one turn game, since normal methods of escaping the problematic, such as moral constraints or intervention of a super powerful actor (e.g., the state), are not available within the context of Diplomacy (and such things would ruin the game or at very least change it beyond recognition).
Another concept that may enable cooperation is the existence of heuristic foci that experienced players may use to reduce the uncertainty of picking which players will make reliable allies. This can simply be reading the way someone speaks, or perhaps more reliably, taking a good look at the map. The designers of standard Diplomacy have evidently placed much effort into making the positions of each power roughly equal. Even so, certain relationships are more natural grounds for alliance than others, especially in the beginning of the game. For example, Italy and Austria make natural allies. Austria faces all but certain elimination at the hands of Turkey and Russia if he attacks Italy at the start. Italy, though he may make quick gains from a quick stab of Austria, will soon face the same problem in protecting his winnings. As the benefits of stabbing each other are in this manner less than going against others, there is an inherent trust possible in an early Austro-Italian alliance.
Finally, this model assumes powers in symmetric positions, something that is fairly rare in Diplomacy play. Actually, when they do occur, the game often ends in a draw, as players calculate the benefits of a 3-way draw compared to the chances of attacking for a win and risking elimination. In many situations, however, unequal power distributions can lead to greater possibilities for cooperation. Particularly when one power is about to achieve victory, the incentive for cooperation and even detailed coordination of moves becomes much greater.
To see this in terms of the model, consider a situation where Player C will win in the next turn if he receives and result better than -3. This could be a reflection of greater power and a small leap needed for victory. In terms of the overall game, players A and B lose more in any outcome set that involves a result for C better than -3, than any payoffs A or B can gain, since they lose the game. In this situation, the strategy set {s14, s24, s34} is no longer an equilibrium. Rather, in this case {s12, s22, s34} becomes the equilibrium with payoffs of 2,2,-4. If either A or B deviates from this strategy set, the result is a victory for C. For example, {s12, s24, s34} leads to -1,3,-2. This is understandable in reference to the overall preference ranking in Diplomacy, where all outcomes save elimination are prefered to survival (the usual result of losing without elimination). However, if for example player A faces elimination if he receives some result lower than 3, {s12, s22, s34} is also no longer an equilibrium. In this case, player A may choose to cooperate with C (which C has an incentive to offer since he need only receive a result higher than -3) to achieve survival over elimination even if this leads to C's victory.

|
David C. Rosen Central European University ( |
If you wish to e-mail feedback
on this article to the author,
click on the letter above. If that does not work, feel free to use the
"Dear
DP..." mail interface.