Diplomacy and International Relations Theory
Part 1
David C. Rosen
The game Diplomacy (© Hasbro, Inc.), a multi-player "war game", may
function as a model to illustrate several forms of International Relations Theory.
Systemic theories such as neorealism, rational actor "Game Theory" and those that
analyze communication and perception seem particularly well suited to the play of
Diplomacy. Neorealism, holds that the of international system is anarchic and that
all actors are
like-units. Formal Game Theory was developed in the context of
other social sciences, notably microeconomics, and applied to the international
system by various theorists over the past few decades.
Formal Game Theory was developed in the context of
other social sciences, notably microeconomics, and applied to the international
system by various theorists over the past few decades. A third of set of theories,
those that apply psychological constructs of perception to international relations,
will be addressed in a second article.
A third of set of theories,
those that apply psychological constructs of perception to international relations,
will be addressed in a second article.
Diplomacy is a seven-player game using a simple political map of pre-First
World War Europe. Each player controls one of seven "powers": England, France,
Germany, Italy, Austro-Hungary, Russia and Turkey. Every power begins the game
in a position more-or-less equal to the others, each controlling three "power centers"
(the exception with four, Russia, suffers from a difficult geographical position).
Twelve power centers begin the game as neutral, controlled by no one. The control
of power centers determines the number of units-armies or fleets-that each
player may field. The goal of the game for each player alike is to expand to control
eighteen or more of the thirty-four "power centers." Point values for full victory
and other possible endings are determined by the "Boardman" rating system.
is a seven-player game using a simple political map of pre-First
World War Europe. Each player controls one of seven "powers": England, France,
Germany, Italy, Austro-Hungary, Russia and Turkey. Every power begins the game
in a position more-or-less equal to the others, each controlling three "power centers"
(the exception with four, Russia, suffers from a difficult geographical position).
Twelve power centers begin the game as neutral, controlled by no one. The control
of power centers determines the number of units-armies or fleets-that each
player may field. The goal of the game for each player alike is to expand to control
eighteen or more of the thirty-four "power centers." Point values for full victory
and other possible endings are determined by the "Boardman" rating system.
The outcomes of all moves are determined by the rules' mechanics; there
are no dice. To be successful, a player must do two things. Firstly, he must
anticipate the other players' moves so as to make the best ones possible himself.
Secondly and more importantly, he must use the specifically provided "diplomacy"
time to persuade, deceive and otherwise get the other players to move in a way that
is beneficial to himself. Thus, the name of the game.
must
anticipate the other players' moves so as to make the best ones possible himself.
Secondly and more importantly, he must use the specifically provided "diplomacy"
time to persuade, deceive and otherwise get the other players to move in a way that
is beneficial to himself. Thus, the name of the game.
Whereas the game's format lends itself to the illustration of several IR
theories, it is worth mentioning that its particulars may limit the efficacy of
Diplomacy
itself as a model reflecting the real international system. For example, the fact
that the decisions of each "state" within the game are made by one and only one
individual removes the internal forces that often determine real state behavior. "In-
the-box" theories of international behavior such as bureaucratic models, "Clash of
Civilization" theory,
For example, the fact
that the decisions of each "state" within the game are made by one and only one
individual removes the internal forces that often determine real state behavior. "In-
the-box" theories of international behavior such as bureaucratic models, "Clash of
Civilization" theory, and various structuralist approaches, will find little or
nothing of
value within Diplomacy. And although players may rely upon their experiences from
previous games, there is no historical context as exists in the real world. Also,
though the game allows for "win-win" alliances of temporary duration, in the end it is
absolutely zero-sum.
and various structuralist approaches, will find little or
nothing of
value within Diplomacy. And although players may rely upon their experiences from
previous games, there is no historical context as exists in the real world. Also,
though the game allows for "win-win" alliances of temporary duration, in the end it is
absolutely zero-sum.
This zero-sum quality of the game is a systemic characteristic particular to
Diplomacy that differs greatly from the real international system. It stems from the
fact that within the game there are no status quo powers; no player may win the
game by preserving the situation, all must seek to expand in order to secure victory.
The result is a much more dynamic situation than that which exists in the real
international system. Finally, Diplomacy is of course only a game, designed for
entertainment and not as a simulation of anything else.
That being said, there are some things about Diplomacy that give it potential
as a heuristic tool. Most importantly, the game's required abilities of persuasion,
deception and raw tactical skill have their indisputable analogs in the "real" world of
state behavior. Beyond that, several characteristics of the game make it particularly
useful for IR theory. The game's situation is played in international "anarchy" with
no power superior to that of the other players. This, and the fact that the different players
control powers that enjoy qualitatively equal capabilities, make the game a very
good neorealist model. The fact that the behavior of each "state" within the game is
determined entirely by one individual is extremely useful in its simplicity for
discussing rational actor models. Indeed, Diplomacy works so well with Game
Theory models that the bulk of this paper will be devoted such analysis. The
game's dependence on communication, cooperation and deception, and the ways in
which these are attempted, also invite application of perception analysis. This will
be attempted in Part II of this paper.
This, and the fact that the different players
control powers that enjoy qualitatively equal capabilities, make the game a very
good neorealist model. The fact that the behavior of each "state" within the game is
determined entirely by one individual is extremely useful in its simplicity for
discussing rational actor models. Indeed, Diplomacy works so well with Game
Theory models that the bulk of this paper will be devoted such analysis. The
game's dependence on communication, cooperation and deception, and the ways in
which these are attempted, also invite application of perception analysis. This will
be attempted in Part II of this paper.
Neorealism and Diplomacy
Neorealism's underlying description of the international system is in many
ways similar to the situation of Diplomacy. Neorealism holds that the organizing
principle of the international system is anarchy, that the unit of importance to that
system is the state. That is, there is no power above or below the logic of the
system itself that dictates or controls the behavior of states. The international
system limits the decisions of the states in such a way that the qualitative
characteristics of each state are unimportant. Quantitative variations in relative
capabilities are the only important differing characteristics of states. Ideologies,
political systems and other internal variations have no significant effect upon how
the international system as a whole operates. States that operate in ways that
contradict the logic of the system are behaving "irrationally" and can be expected to
suffer negative outcomes.
This description would serve to describe the game of Diplomacy fairly well.
With no extra-actor mechanisms for dictating or limiting behavior (outside of the
actual rules), the "system" of the game can be accurately characterized as anarchic.
And with only one player per state, there are no forces from "below" that seek to
shape player behavior (multiple-personality disorder?) Finally, every player uses the
same types of power and methods in order to forward their interests. The only
variation between players that occurs at any given time can be expressed in terms
of varying capabilities, in this case in the form of power centers and units
controlled.

Thus, many theories of neorealism should be applicable to Diplomacy. This
paper will not attempt to cover all of them. Instead it will concentrate on just a few
that seem to have particularly apt parallels within the game. These concepts are the
"security dilemma," balance of power behavior and the "band-wagon" phenomenon
that is covered in the neorealist sub-theory of hegemony.
The first concept of neorealism, inherited from classical realism, that can be
easily found in Diplomacy is that of the "security dilemma." That is that forces built
to defend against the potential threat of other actors may cause those other actors
to feel themselves threatened. Diplomacy provides an excellent example of this
phenomenon. The security dilemma is all the more "real" in Diplomacy given the
fact that all players are inherently expansionist.
Units used for defense of territory are precisely the same units that are used
in offensive action to gain new territories, often at the expense of neighboring
powers. Thus any unit is always simultaneously a force for defense, and a force of
threat. The security dilemma also applies to territorial position. The best defensive
positions for a given player are always forward, so that other powers have no units
adjacent to that player's power centers. At the same time, those forward defensive
positions are unavoidably near someone else's power centers, and therefore always
constitute a potential threat. And this threat is usually not only perceived; a good
player always considers the potential of all of his units to improve his overall
strategic situation. Even if the defensive position is against an "ally," those units
provide both a coercive element to diplomacy towards that ally, and the possibility of
a quick "back-stab" if the player sees such a move as providing more benefits than
the alliance itself.
A second concept of neorealism, also inherited from classical realism, that
applies to Diplomacy is balance of power. Players that successfully expand become
more powerful as they do so, eventually becoming unstoppable. This inevitably
results in attempts by the other players to balance an emerging victor. The larger a
given power becomes, the more likely his allies will defect to a balancing coalition.
Victories usually occur when other players, in the pursuit of their own short-term
interests, fail to defect in time. This failure of balance of power within game play
is not a perfect parallel of the failures found in real world balances that stem from
over-rigid alliances. While that is a factor, the need for all players to expand
inherent to Diplomacy is equally the cause. The decision of when to defect from
alliances will be discussed further in the Game Theory section below.
The last concept of neorealism discussed in this paper, from the sub-theory
of hegemony, is a variant of balancing theory most developed by Steve Walt in
eighties. Walt asserts that in some cases, small powers have rational reasons not
to pursue balancing behavior against a large, threatening power with hegemonic
aspirations. If the costs of joining a balancing coalition are seen to be much higher
than the costs of cooperating with the hegemon, the small state will "band-wagon"
with the winner. In Diplomacy this occurs when a player believes that he has little
or no chance to participate in a draw, and that cooperating with the emerging victor
gives the best chance of survival. Since survival offers a higher benefit in terms of
Boardman points than elimination (one versus one-half, respectively), players often
decided to help a victor, even when such help will end the game.
Game Theory and Diplomacy
Game Theory, as might be expected from its name,
has many possible applications to Diplomacy. In fact, there are so many that this
paper will only endeavor to explore a few models that I feel are the might be useful
or interesting in discussion of the game.
In order to expand in Diplomacy it is all but necessary to work with another
power. Two equal powers attacking each other without third-party support inevitably
results in stalemate, which, since the other players will be attempting to expand at
same time, usually results in the relative decline of both deadlocked players. Thus,
alliance-making, either short-term or long-term, is the generally the first order of
business in Diplomacy.
Game Theory holds that alliances form when ever two or more actors
determine they will receive more benefits in coalition than each would do by "going it
alone." A given actor will choose to ally with the other actor or actors that he feels
will provide the greatest benefits, of those that wish to ally with
him.
 An relatively
weak actor may also seek alliance to prevent being swallowed; the more vulnerable
an actor is, the more likely he is to seek allies. In Diplomacy, the alliances that
form
in the beginning follow these patterns.
An relatively
weak actor may also seek alliance to prevent being swallowed; the more vulnerable
an actor is, the more likely he is to seek allies. In Diplomacy, the alliances that
form
in the beginning follow these patterns.
The map and game experience give a framework of which alliance
configurations tend to work best. Thus, for example, active alliances between
France and Turkey are unusual in the beginning of the game, because there is little
the two can do for each other. Germany nearly always seeks to ally with either
England or France, as if those two ally against, him, his prospects for survival, let
alone winning, become very dim.
Game Theory predicts that the size of alliances are limited by rationality to
the smallest size possible to determine positive outcomes. Given for example, 5
equal actors attempting to divide say 12 items of value,
 when any three can
determine the whole distribution, the final coalition will not be larger than 3:
when any three can
determine the whole distribution, the final coalition will not be larger than 3:
Four-way coalition:
(3,3,3,3,0)
where each number corresponds to the value-items enjoyed by each actor.
Three-way coalition:
(4,4,4,0,0)
Any three actors will prefer to exclude a fourth from participating to increase
the value of their rewards, thus making the first coalition more desirable than the
second. Of course, the two actors left out may offer one of the other actors an
incentive to break the coalition by offering a higher reward: (6,0,0,3,3). This
results
in alliance instability, as at that point, one or both of the new "out" actors may
offer
other distributions to salvage something, such as (0,2,0,5,5) or (8,2,2,0,0).
This shifting can go one indefinitely as long as there is no cost to
redistributing the value-items, and system retains the ability of any three actors to
determine all outcomes. However, as in the real world, in the game of Diplomacy
being able to redistribute resources at will is not possible. Also, especially in
Diplomacy, the number of actors required to impose a distribution changes as each
actor's share of item-resources (in this case power centers) changes. Thus, early
alliance distribution divisions tend to be firmer, and decisions to shift alliances
offer
their own risks and rewards, perhaps best illustrated with another Game Theory
model, the Prisoner's Dilemma, which this paper will examine further on.
Still, given the limiting factors, the underlying logic of alliance-size
minimization holds true in Diplomacy. For example, in the early and middle game of
Diplomacy, this alliance limiting behavior can clearly be found. A good example of
this can be found in attempts to conquer Russia. That player is particularly
vulnerable to hostile alliances. Turkey, Austo-Hungary, Germany and England are
all in better position to attack Russia than they are to help or be helped by it. But
the Game Theory predicted limitations on alliance size lends some hope to Russia.
All four threatening powers, by working in concert, can easily dispatch Russia. But
the spoils to be gained in conquering Russia are marginal if dived by four. If one
includes all four starting Russian centers, and adds the typical Russian neutral
conquests of Rumania
 and Sweden, there are six power centers to be gained from
the conquest of Russia.
and Sweden, there are six power centers to be gained from
the conquest of Russia.
First of all, power centers cannot be divided. Thus, a division by four powers
will result in inequalities.

 In conquering Russia with a four-way coalition, the
expected yield for each player will be (2,2,1,1). This is an inherently unstable
division, and better yields are available with other combinations; three powers can
usually conquer Russia without the aid of a fourth, providing larger shares of spoils.
A three-way coalition yields (2,2,2,0). When two try to do the job alone, the best
they can hope for is (3,3,0,0), but as Russia will have good grounds for appealing to
those gaining nothing, their yield will likely be far less. They may even suffer a net
loss if the result is a coalition including Russia against them. Thus, if an alliance is
to form against Russia, it will be most successful if exactly three players
participate.
In conquering Russia with a four-way coalition, the
expected yield for each player will be (2,2,1,1). This is an inherently unstable
division, and better yields are available with other combinations; three powers can
usually conquer Russia without the aid of a fourth, providing larger shares of spoils.
A three-way coalition yields (2,2,2,0). When two try to do the job alone, the best
they can hope for is (3,3,0,0), but as Russia will have good grounds for appealing to
those gaining nothing, their yield will likely be far less. They may even suffer a net
loss if the result is a coalition including Russia against them. Thus, if an alliance is
to form against Russia, it will be most successful if exactly three players
participate.
Alliance size limitation is clearest in the draw mechanism of Diplomacy.
While the rating system strongly encourages solo wins, it is possible to "share"
victories. When victories are shared, the rating system encourages winning
coalitions to be as small as possible:
| Winning coalition size | Boardman Points for each victor 
|
|---|
| 7 | 1
|
|---|
| 6 | 1.17
|
|---|
| 5 | 1.4
|
|---|
| 4 | 1.75
|
|---|
| 3 | 2.33
|
|---|
| 2 | 3.5
|
|---|
| 1 | 7
|
|---|
The question of when to defect from an alliance is critical to Diplomacy play.
To win the game outright, it is all but impossible to remain loyal to all parties
throughout the game. Also, as a player approaches victory, he must be aware that
it will becomes more likely that his allies defect. It always better that he defect first,
to make quick gains therefrom, and to prevent the other players from critically
weakening him. The situation on any given turn resembles a Game Theory
Prisoner's Dilemma, with several extra-dimensions.
The Prisoner's Dilemma is familiar to many, so only a brief description will be
given here. Two prisoners, A and B, have been arrested by the police on suspicion
of a serious crime, say murder. They are placed are interrogated separately, and
given no chance to communicate with each other. Each faces an identical choice.
Each may work with the police, or maintain solidarity with his comrade. The
consequences of each choice depends on what the other chooses. If A cooperates
with the police and B doesn't, A receives a very light sentence on a lesser charge,
and B receives death. If the reverse occurs, B gets off lightly, and A will face the
executioner. If both choose to cooperate, both will receive heavy sentences. If
neither talks, then they will each receive moderate sentences. A matrix illustrates
the possible outcomes:
| Prisoner B
|
|---|
| Prisoner A | Solidarity | Defection
|
|---|
| Solidarity | (b,b) | (a,d)
|
|---|
| Defection | (d,a) | (c,c)
|
|---|
a,b,c,d are outcomes for each prisoner in the sequence of A,B, in alphabetical order
of desirability where a stands for a light sentence, b for a moderate sentence, c for a
heavy sentence,
and d for a death sentence.
As a rational actor, A will always choose defection. For he will reason that if
B chooses solidarity, defection is the better choice because it will result in outcome
a, as opposed to b. If B chooses to defect, then defection is better because it will
result in outcome c rather than d. Either way, defection is the best choice for A.
Since B, as another rational actor, will reason similarly, this situation will always
result in both prisoners cooperating against each other, even if both prisoners
choosing "irrationally" would result in a better final outcome.

In different situations that occur during the play of Diplomacy, different
decision combinations provide different yields. Not all of them can be represented
by a simple transference of the Prisoner's Dilemma, but that is a good place from
which to start. In the beginning of the game, when all players are seeking to
expand, and no player is in a position to make progress alone, one version of the
matrix looks like this:
| Player B
|
|---|
| Player A | Maintain Alliance | "Back-stab"
|
|---|
| Maintain Alliance | (a,a) | (b,d)
|
|---|
| "Back-stab" | (d,b) | (c,c)
|
|---|
"a" here represents a strong potential for gains against players C,D,E,F
and/or G, "b" represents potential initial gains against the other player,
limited without outside help,
"c" represents a stalemate position, relative decline versus players C,D,E,F
and G, and
"d" represents a vulnerablity to losses or elimination.
In this case, since the yield will always be higher by sticking to the alliance,
that result can always be expected. This matrix applies when A or B have no option
to ally with C. However, this is not usually the case. If, for example, A has the
option of allying with C, a different outcome can be expected:

| Player B
|
|---|
| Player A | Maintain Alliance | "Back-stab"
|
|---|
| Maintain Alliance | (a,e) | (b,h)
|
|---|
| "Back-stab" | (d,f) | (c,g)
|
|---|
where a,b,c,d are all outcomes for A, e,f,g,h are all outcomes for B;
 outcomes a and b are of equal preference to A:
a=strong potential for gains against players C,D,E,F and/or G,
b=strong potential for gains against player B,
c=no longer a stalemate position, the alliance with C allows for gains against B, but
the position will not be as good as if B had not moved against A,
d=A has not successfully consummated an alliance with C, and now is in a bad
position against B,
e=strong potential for gains against players C,D,E,F and/or G,
f=good position versus player A, and A not allied with C,
g=now under combined AC attack, possible losses,
h=completely vulnerable to AC attack, certain losses, possible elimination.
outcomes a and b are of equal preference to A:
a=strong potential for gains against players C,D,E,F and/or G,
b=strong potential for gains against player B,
c=no longer a stalemate position, the alliance with C allows for gains against B, but
the position will not be as good as if B had not moved against A,
d=A has not successfully consummated an alliance with C, and now is in a bad
position against B,
e=strong potential for gains against players C,D,E,F and/or G,
f=good position versus player A, and A not allied with C,
g=now under combined AC attack, possible losses,
h=completely vulnerable to AC attack, certain losses, possible elimination.
In this situation, A will choose to ally with C, and the result will be both A and
B "back-stabbing" each other. This is because A will see that if he decides to
maintain the alliance, the result for him will be either outcome a or outcome d,
whereas if he "back-stabs," the result will be either outcome b or c. Since outcome
a is equal to outcome b, the value of second set as a whole is higher. Because B
will know the logic of A's situation, he will also choose to "back-stab," so as to face
outcome g rather than h. Thus, the final outcome will be c for A and g for B. Just
as in the traditional prisoner's dilemma, the rationality of each position dictates a
final outcome that is less than the best possible outcome for each player (in this
case a,e).
Alliances that have been functioning successfully tend to continue to
function successfully, since each player becomes more sure of the other's likelihood
of maintenance and wants to continue to enjoy the "win-win" benefits from the
alliance. This remains the case until one of several things happens. For example,
one of the players, reacting to a new opportunity provided by changes in the game
situation, may perceive that there are higher gains to be made by "back-stabbing"
the other. A player may determine that he cannot win without taking his ally's power
centers. Or player might determine that his ally will win the game, resulting in his
own loss, if he continues the alliance. Finally, a player may come to the conclusion
that his ally is thinking along the lines of any of the previous rationales, and decide
to "back-stab" first to avoid losses. All of these are dynamic values that change as
the game board situation changes.
For this last attempt at analyzing Diplomacy Game Theory, this paper will
attempt to create a formula, based on these factors, to describe A's decision
of whether or not to "back-stab" B:
(b(g+o)) - (e(s+r)) = 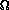
where
-
- b=0 if A believes B will "back-stab"; 1 if not,
- g=the gains to be made by continuing the alliance,
- o=the perceived increase in threat from other players if B is no longer an
ally,
- e=0 if A expects to be eliminated if it "backstabs" B and b=1; 1 if not,
- s=the proportion of the spoils A expects to get in a successful attack
against B,
- r=the risk perceived that B will reach "the point of no return" toward
victory, and
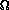 =behavior of A, where a positive number means A maintains
the alliance with B,
and a negative number means A "back-stabs" B.
=behavior of A, where a positive number means A maintains
the alliance with B,
and a negative number means A "back-stabs" B.
As long as the balance here remains positive (more gains than perceived
risks and other rewards), A will remain loyal to the coalition. If the result is
negative,
A will "back-stab" B. If equation balances, the decision can go either way. Changes
in several of the variables can cause A to decide to "back-stab" B.
If A believes that B will "back-stab" (b=0) he will follow suit no matter what the
other variables. The value of the gains to be made from continuing the alliance (g)
becomes nullified as the alliance will be finished in any event. By the same token,
the protection that the alliance with B offers from the other players (o) becomes
nullified as well. The expectation of elimination resulting from attacking B
(e) will no
longer matter either since inaction will not prevent elimination either.
Since the risk
that B will reach "the point of no return" (r) will always be positive, even if
negligible, the decision to "back-stab" B will always be made, regardless of the
spoils to be
gained for A (s).
If the gains to be made from the alliance (g) drop to little or nothing, A
becomes far more likely to "back-stab" B. But this will not occur if A expects not to
survive such an action (e). Also, if the risk that B will win (r) is low and the
gains to
made by attacking B are also very low (s), even a low profitably AB alliance may
survive, especially if A feels that the outside threat from other players and the
alliance with B is vital in this way (o).
If A sees that any attack on B will result in his own elimination (e), he will not
follow such a course, no matter how high are the spoils to be gained and/or the risk
of B winning (survival is worth twice as much as elimination). A will instead choose
to "band-wagon" as in the neorealist theory, and maintain the alliance to the end.
The only rational reason to ignore this variable is if A expects B it attack him.
If B leaves himself particularly open to attack, and/or other players come to A
with tempting proposals of how to carve B up, A will be more likely to "back-stab" B.
This will be a factor of how much of the spoils A expects to receive (s). Of course,
if
A sees that he only needs a small push to himself reach victory, the relative value of
even one center may be much higher, and thus encourage a "back-stab." At the
opposite end of the spectrum, if A sees such an attack on B leading to his own
elimination, that consideration will outweigh the incentives to attack. And if A
thinks
he has more to gain by sticking to the alliance (g) than by attempting a grab at B's
power centers, the temptation will be resisted. The same will occur if A feels that
the moment B is swallowed, A will be alone and critically vulnerable to the attacks of
the remaining players (o).
Finally, a critical point in the game occurs when one player has amassed
enough power centers to provide an imminent threat of victory. However, it is
difficult to determine when this point has been reached. Whether or not the players
are able to determine this point usually determines if a bid for victory will succeed.
The risk that further cooperation with, or even a failure to oppose B will result in a B
victory (r) is critical to the decision to "back-stab." When this factor becomes large
enough, nothing, including even large gains to be made by A if the alliance is
continued (g), will stop A from "back-stabbing" B, except for the fear that such action
will result in his own elimination (e).
Most of the variables can be determined in part by studying the situation of
the board. Especially, variables (e) and (r) are best determined that way. But the
others also require and an ability to "read" the feelings of the other players. To
some extent, it is possible to predict the other players' behavior by applying the
same formula to their situations. But often the results determined by such an effort
will provide no certain answers. Instead, a player has to rely upon other cues. That
is where successful communication and deception come into play, and where Game
Theory, and Part I leaves off. Perception theory and cognitive approaches will be
taken up again in Part II.
Conclusion
Insofar as the game provides a useful model of social interaction of actors
with differing interests pursuing non-complimentary goals, the events within the
game itself can be useful in discussions of much larger patterns of human behavior.
If what goes on in the interaction between seven game players "fighting" over a
virtual map of pre-World War One Europe has any resemblance to the real
international system, than IR theories of Neorealism and Game Theory have some
validity. For their models are very instructive when applied to the game of
Diplomacy.
If there are no useful parallels between Diplomacy and the real international
system, I hope that this paper was at least able to demonstrate how some theories
of IR might be applied to how systems in general work. And, if nothing else,
perhaps some Diplomacy players reading this paper might have luck in improving
their games.
If you wish to e-mail feedback on this article to the author,
click on the letter above. If that does not work, feel free to use the
"Dear DP..." mail interface.


 Formal Game Theory was developed in the context of
other social sciences, notably microeconomics, and applied to the international
system by various theorists over the past few decades.
Formal Game Theory was developed in the context of
other social sciences, notably microeconomics, and applied to the international
system by various theorists over the past few decades. A third of set of theories,
those that apply psychological constructs of perception to international relations,
will be addressed in a second article.
A third of set of theories,
those that apply psychological constructs of perception to international relations,
will be addressed in a second article.