Introduction

My previous article in the Diplomatic Pouch explored the beginning of a Diplomacy game. Using statistical analysis, I answered the following questions: What supply centers is each Power likely to capture in 1901 and 1902? and How well does each Power do, in the long term, if it captures a given supply center?

That's all well and good for 1901 and 1902. But what about 1903? What about further on down the road, when the game is winding down and someone is hoping to pull off a victory? Can statistical analysis tell us what tends to happen at the end of a Diplomacy game? Of course it can.

What does Victory Look Like?

As a Diplomacy player, your ultimate objective is winning the game, which (in the Standard variant) means gaining control of 18 supply centers. From the very beginning of the game, you should be thinking about how to achieve this objective. What will your 18 centers be? How long will it take you to get to them? Which of your six competitors are going to help you out, and which ones are you going to bump off?

The answers to these questions depend heavily on who your opponents are and how your rapport with them develops. Do not hurry to formulate your plan before getting to know the other players. On the other hand, you cannot escape a certain element of geographical fate. If you're England, you'll likely need to count the German home centers among your 18; and as a consequence you may have to eliminate Germany, even if you get along great with the German player. But you probably won't need the Italian home centers (although you may need to attack Italy in order to take other centers from him), and you almost certainly won't need the Turkish centers. So go ahead and negotiate an alliance with the Kaiser; just keep in mind that your chances of victory are low unless you mercilessly backstab him and destroy him utterly. But he doesn't have to know that.

In this article, I will present data from FRIGATE, my trusty statistical-analysis tool. I will answer the following four solo-victory-related questions:

• Who wins most often? How often does each Power solo? How does this depend on the press type?
• How long does the game take? How many game-years occur before the game officially ends? How does it depend on the game's outcome, or on the press type?
• Which supply centers do Powers usually win with? What portion of a Power's solo victories include control of a particular supply center? For example, how often does Russia count Greece among his magic 18 (or 19, or 20)?
• How often do Powers eliminate other Powers on their way to victory? What portion of a Power's solo victories entail the elimination of certain other Powers? For example, how does an Italian solo correlate with survival for Austria?

Results & Analysis

Who wins most often?

These results parallel the findings in my first article. No-press games are more likely to end in solo victories than games with press. France is by far the most likely victor, although Russia earns the most solos in full-press games. Italy and Austria are the hardest Powers to win with, regardless of press type. Russia wins more often in games with more press, while France, Germany, and Turkey benefit from less press.

When does the game usually end?

Note that these averages are actually medians, rather than means. This reduces the effect of outliers (i.e. the occasional game that continues until 1952, which distorts the mean.) It also ensures that the data is almost always in the easy-to-digest form of whole numbers.

The game-length numbers here depend on two variables: press type and game outcome. Table 2 shows that more press tends to make a game go more quickly, which makes perfect sense: it's easier for players to cooperate in a press game. Without press, you can agree to ally with your neighbor but still be unable to coordinate your units, because you have to guess how your ally is going to move. As a result, your own moves will inevitably involve guesswork, resulting in a lot of bouncing and other unproductive movement.

Games ending in solos are likely to wrap up at about the same time as games ending in draws. This is surprising; one would think that solo games end sooner. After all, a drawn game is often the result of a failed attempt at a solo, and these games may continue for many game-years after a draw becomes inevitable, because the player trying to solo won't give up. These data suggest a counterbalancing factor: some games are declared draws well before the draw is inevitable. Perhaps some of us are giving up on our solo chances a little bit too soon, or accepting a large draw when we could fight for a smaller one.

Lastly, some Powers take longer to get to 18 than others. The Russian steamroller is notably fast; Russian solo victories take place one or two years before everyone else's. The English are a year slower than the others, perhaps because of the necessity of setting up convoys onto mainland Europe. The other five Powers are virtually equal in speed.

Which supply centers do Powers usually win with?

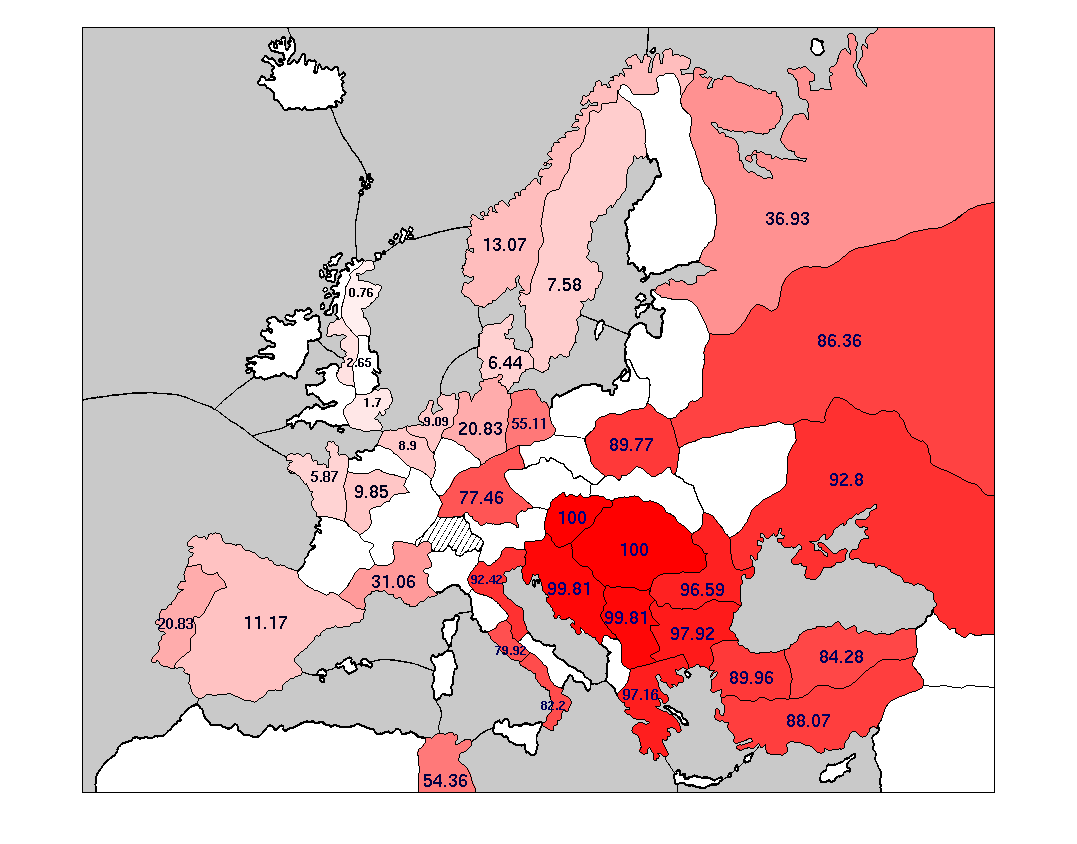
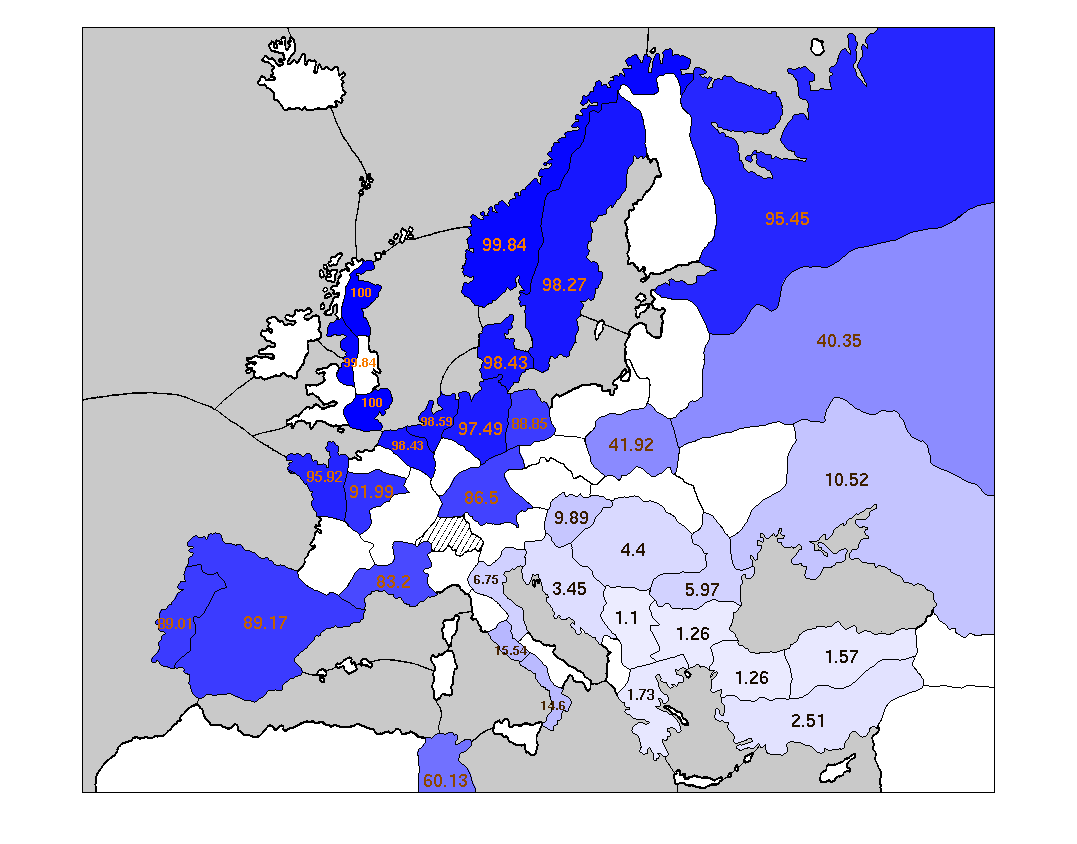
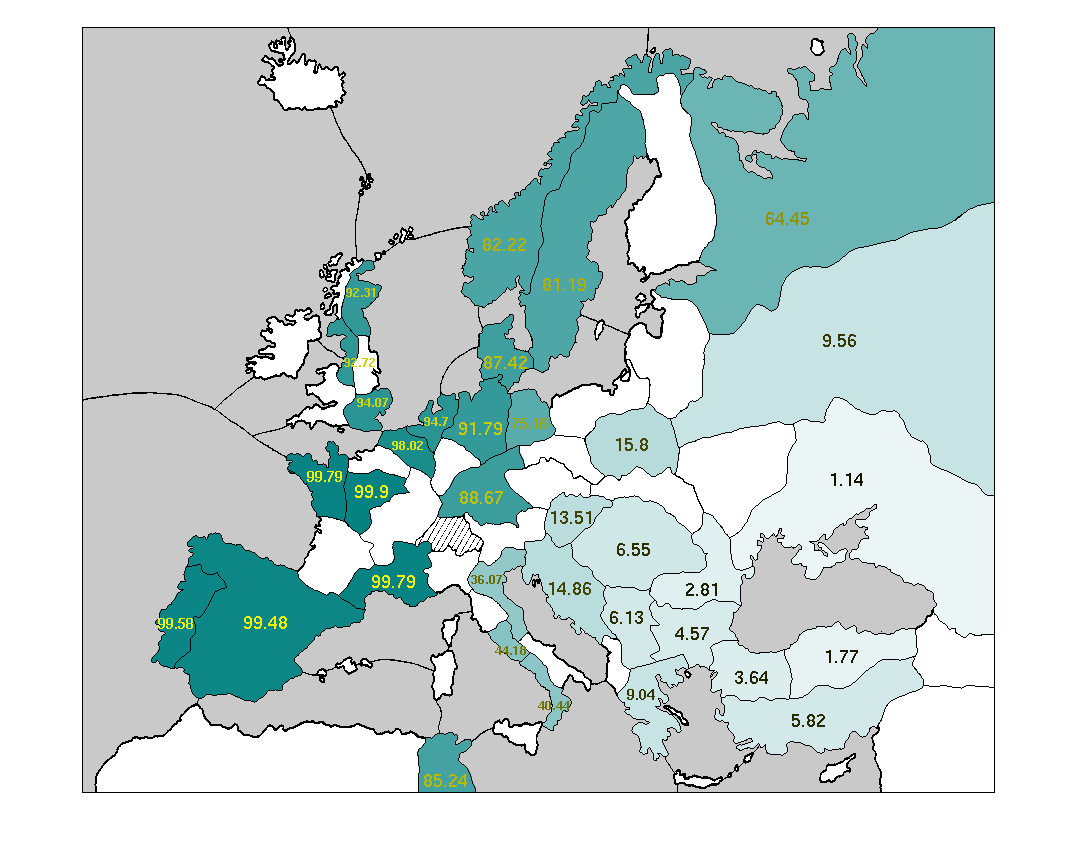
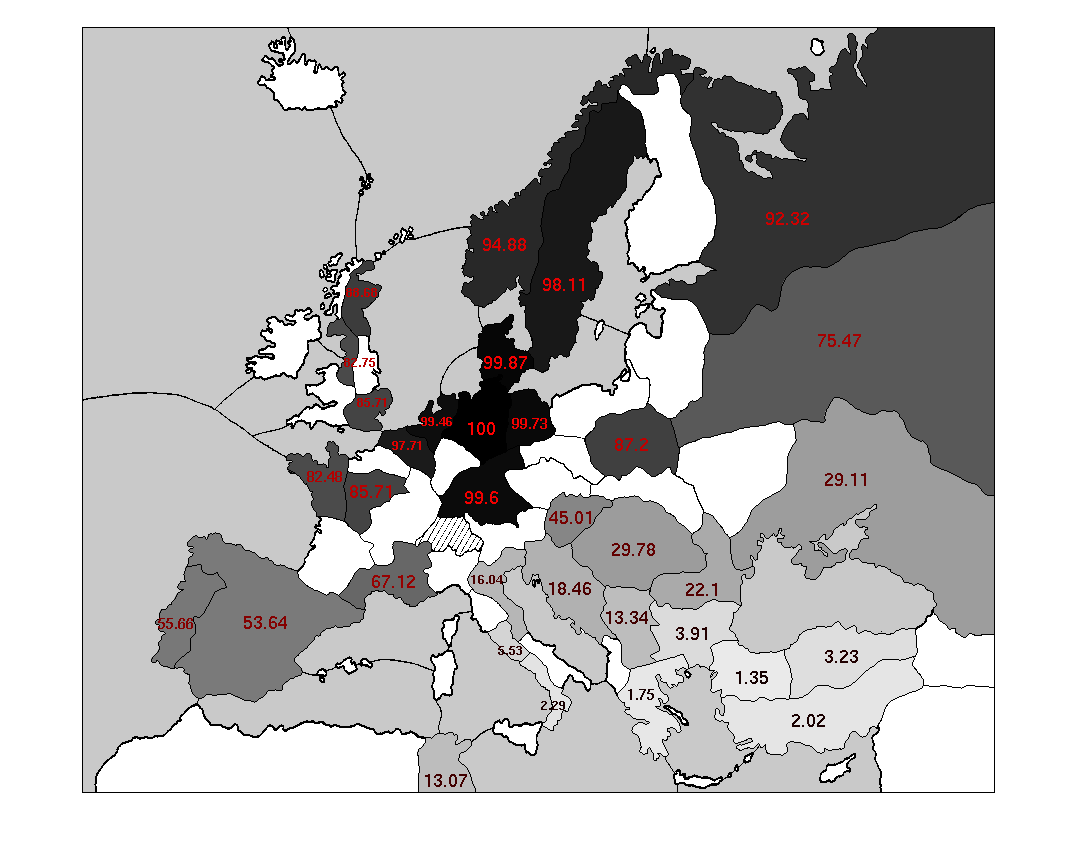
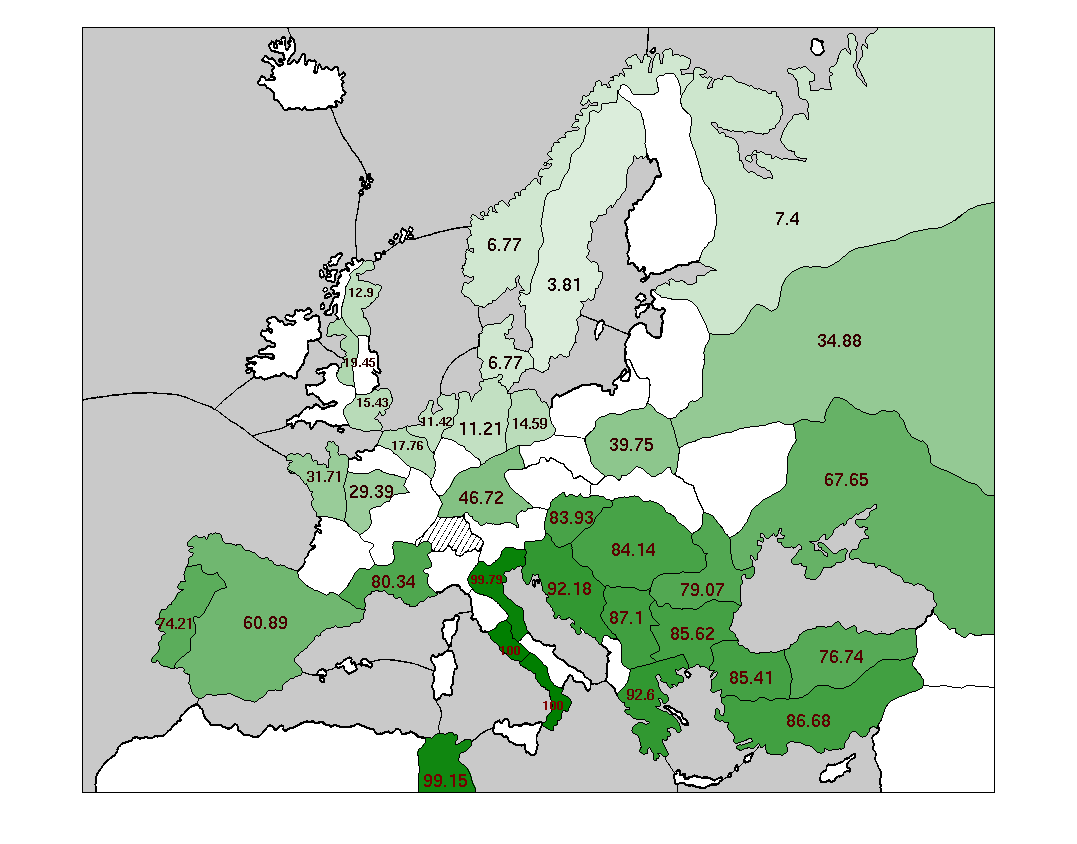
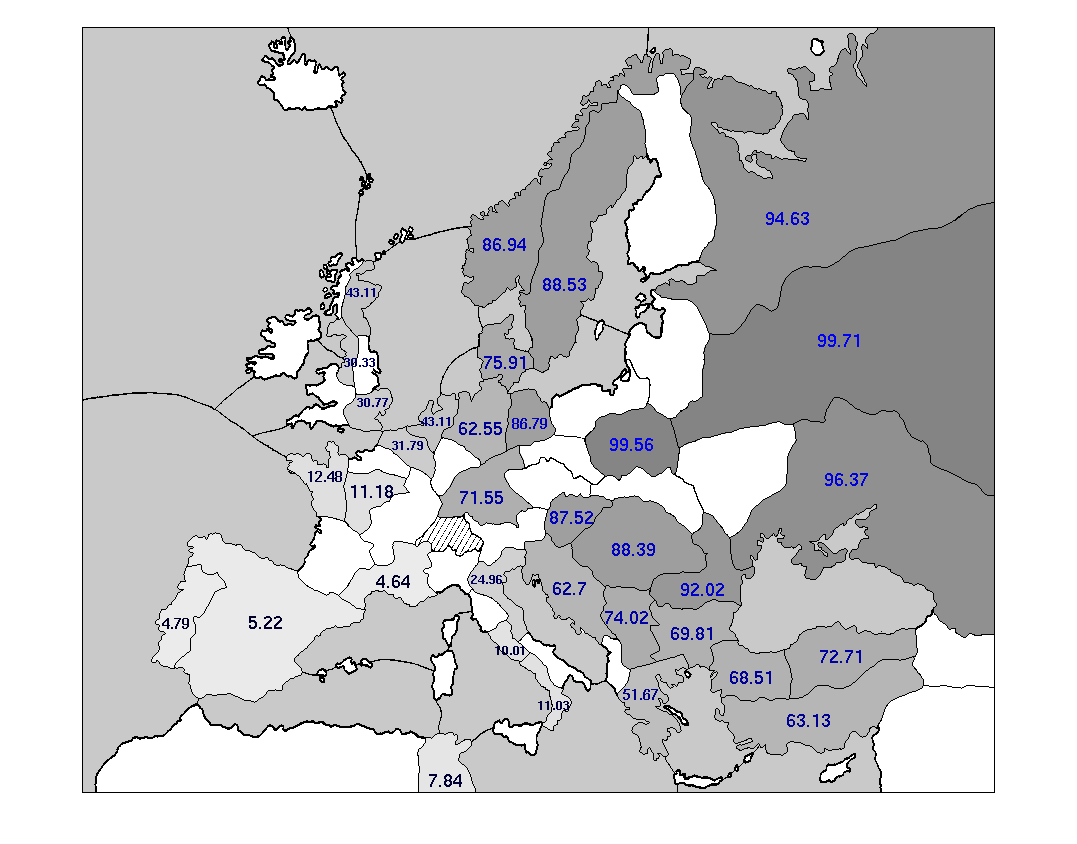
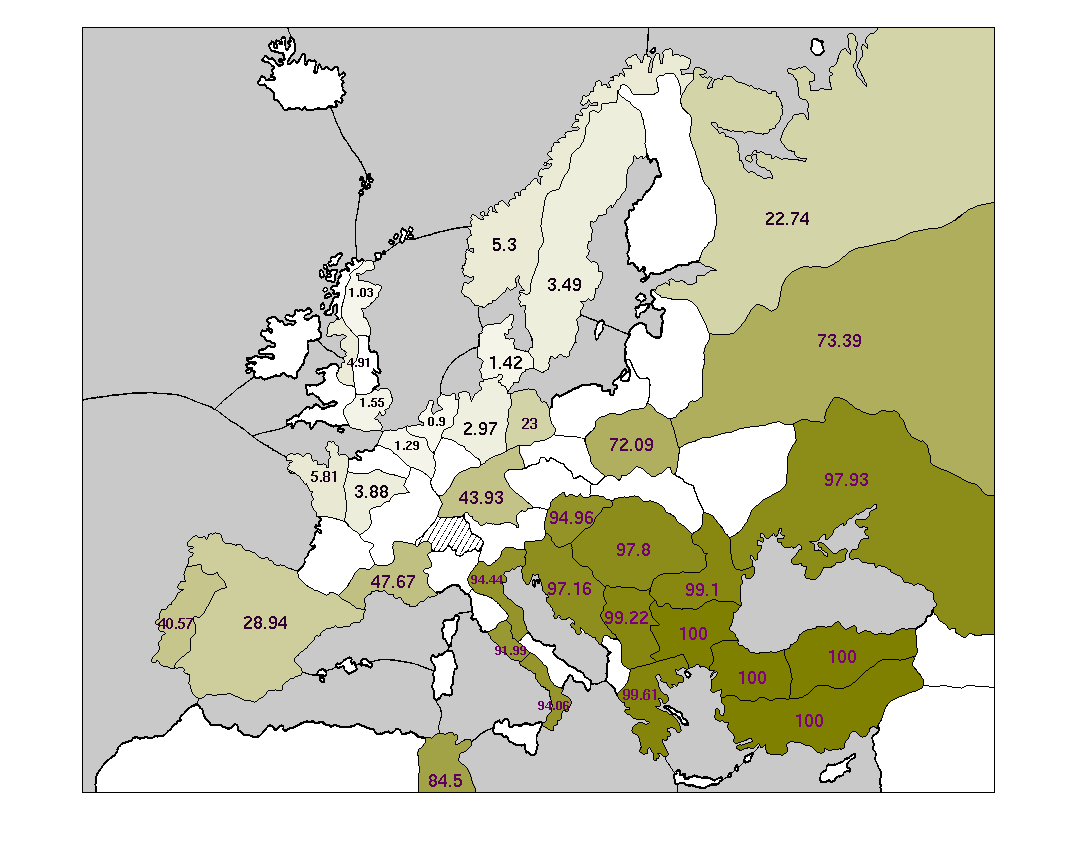
A picture is worth a thousand numbers. The most effective way to show the raw data for this question is not with another huge chart, but with colorful maps. Here are some maps showing the centers typically owned by each Power when it achieves a solo victory.

Some words about the coloration of these maps: every supply center is colored with an intensity matching the probability of that Power occupying the center in its victory year. The probability is also written on to each supply center, expressed as a percentage.

These maps suggest that, in solo victories, anything is possible. Every single Power owns every single center at least sometimes. On the other hand, some positions are much more likely than others. Specifically: most solo victories are heavily concentrated on one side of the main stalemate line.

As an experienced Diplomacy player will know, the main stalemate line (hereafter abbreviated MSL) separates a set of 17 northern and western supply centers from a distinct set of 17 southern and eastern centers. The northern centers include the English, French, and German home centers; the Iberian, Lowland, and Scandinavian neutrals; and St. Petersburg. The seven Great Powers include three exclusively northern Powers (England, France, Germany) and three exclusively southern Powers (Italy, Austria, Turkey). Russia is often lumped in with the southern Powers, although it is more ambiguous than anyone else on the board, since it owns home supply centers on both sides of the line. The primary feature of the MSL is that supply centers on one side of it are easily defended, by means of a stalemate line, from attacks originating on the other side. Conversely, it is hard to break across the MSL and capture centers on the far side of it.

The power of the MSL is borne out in these maps. Every side-bound Power (i.e., not Russia) occupies the centers on its own side of the MSL much more frequently than the centers on the far side. The "Wicked Witches", England and Turkey, are far away from the MSL and are particularly susceptible: each is significantly more likely to occupy any center on its own side of the MSL than any center on the far side. These differentials are not purely the result of increased distance to the far-side centers: note that France is almost twice as likely to take St. Petersburg (four turns away at best from any French home center) as Venice (two turns away from Marseilles.)

Of course, you cannot win by adhering completely to one side of the MSL, since each side has only 17 centers. To win, you have to break across the MSL and grab at least one center on the other side. But what center is that likely to be? The answer is different for each Power, and it relates closely to the Powers' typical army/fleet makeup.

• Austria is heavily land-based, and often has trouble building up a navy. So the dry regions of central Europe are his best chance to break through. Austria takes Munich and Berlin quite often — more often, in fact, than Tunis, which is on his own side of the MSL but requires naval power to capture.
  
  
• England is the opposite of Austria: heavily naval. Hence Tunis, which is Austria's toughest reach on the southern side of the MSL, is England's easiest pickup there. England may also win by bringing armies through St. Petersburg — the quickest convoy route to the MSL — and muscling into Warsaw and Moscow.
  
  
• France can push into the Mediterranean more easily than England, because he can build fleets there. As a result France is very likely to take Tunis. Beyond that, his three most common pickups in the south are the Italian home centers. This suggests that France's high solo frequency may be directly attributable to his ability to build fleets in Marseilles.
  
  
• Germany is more land-based than his neighbors England and France, which makes his winning mix of centers different from theirs. He is less likely to break into the Iberian peninsula and much more likely to take the landlocked centers to his east, including Warsaw, Moscow, and Vienna.
  
  
• Italy is the second most likely Power to make a significant break across the MSL, after Russia. He usually dominates the Mediterranean with his fleets and gets Marseilles, Spain, and Portugal. However, the Italian armies reach Warsaw and Moscow with less than 40% frequency, an unparalleled low for a Power taking centers on the close side of the MSL.
  
  
• Turkey has a good mix of armies and fleets, but his fleets are typically bottled up in the Mediterranean and can't help out in the Scandinavia/Baltic area. Turkey tends to win by pushing into Marseilles or Munich, or, if he can manage to get a fleets out into the Mid-Atlantic, grabbing Portugal.

How often do Powers eliminate other Powers on their way to victory?

These numbers are a little tricky to interpret. Each Power has some generalized probability of winning, which is an average within the dataset of all games. Each Power's probability of winning changes when the dataset is restricted to games in which a particular other Power survives. (Note that "survival" is not the same thing as "not losing". You can lose without being eliminated if another Power achieves a solo, or if you get shut out of a No DIAS draw.)

For example, Germany solos in 8.0% of all games. Among games in which Turkey survives, however, Germany solos 12.6% of the time. This is strong evidence of a spoiler effect: Germany and Turkey have some common neighbors, so if Turkey is eliminated, some of Germany's neighbors get stronger and are more able to keep him at bay. A feisty Turkey, though, can distract other Powers, who then become unable to prevent a German solo. Germany actually has an incentive to ensure Turkey's continued survival through diplomatic means.

This chart of raw data is not a succinct way to answer our questions. If you're playing Italy, and you're trying to decide whether to take down Austria, you want to know if an Austrian bloodbath improves your chances. How much more likely is Italy to solo if Austria is eliminated? For that matter, Austria might be a threat to you, and you want to know if he's got designs on you: How much more likely is Austria to solo when Italy is eliminated? Let's define a statistical value, the mutual antagonism, as follows: two nations have a mutual antagonism equal to the amount that survival by one Power decreases the probability of a solo by the other Power. The number is averaged over both Powers, and normalized by their total probability of winning. For example, Austria and Italy have a mutual antagonism of
[ (5.9% - 6.6%) + (5.1% - 3.2%) ] / (5.9% + 5.1%) = 11.3%

Table 4:
Mutual Antagonism for Solo Victories

	England	France	Germany	Italy	Russia	Turkey
Austria	-59.1%	-24.6%	-36.8%	11.3%	36.5%	79.4%
England		62.0%	58.2%	-13.8%	-2.4%	-52.6%
France			33.2%	-24.4%	-55.6%	-42.8%
Germany				-50.3%	14.5%	-48.8%
Italy					-52.1%	59.6%
Russia						4.1%

Color spectrum:

If you wish to e-mail feedback on this article to the author, and clicking on the envelope above does not work for you, feel free to use the "Dear DP..." mail interface.