The convoy paradox in Diplomacy may show up in connection with convoyed attacks and the rules for the cutting of support. Fortunately it happens quite rarely in practical games, but the problem is fascinating and it should be possible to find a solution.
The purpose of this article is to show what has been done to prevent these paradoxes, and to suggest an addition to the rules which prevents paradoxes from happening and does not introduce unacceptable or illogical results.
To set the foundation, we have the two general rules about the cutting of support. Firstly:
If a supporting unit is attacked from a different field than the one into which it is giving support, the support is cut and does not take place.
And the second rule:
If a supporting unit is attacked and dislodged from its field, the support is cut even if the dislodging attack comes from the field into which it is giving support.
I think it is very important that these rules are kept without modifications during the search for ways of solving the paradoxes described below.
Now, let's start by looking at a simple paradox:
England: Fleet Wales – English Channel; Fleet London supports Wales – English Channel.
France: Army Brest – London; Fleet English Channel convoys Brest – London.
England may state that the supported attack on English Channel dislodges the French Fleet so that the convoy doesn't take place. France, on the other hand, may state that the attack on London cuts the support for the attack on English Channel so that the Fleet there is not dislodged and the convoy is possible.
To solve this paradox, a rule was added (Edition Avalon Hill 1976):
If a convoyed army attacks a fleet that is supporting an attack on the convoying fleet, that support is not cut.
The justification for this solution is that the convoyed attack, so to speak, comes from the field into which the support is given, even if the army really comes from a coastal province some fields away. You may say that the question of cutting support is handled roughly as if it was the convoying fleet itself that made the attack. Another justification, in my opinion, is that the attack on the convoying fleet takes place before the convoyed army reaches shore and begins its attack on the supporting fleet. In other words, the attacker’s support is already given by the time the support cutting takes place.
This rule solves the paradox by resolving that the French Fleet is dislodged from English Channel, and the convoy doesn't take place.
Now let's add the following to the example:
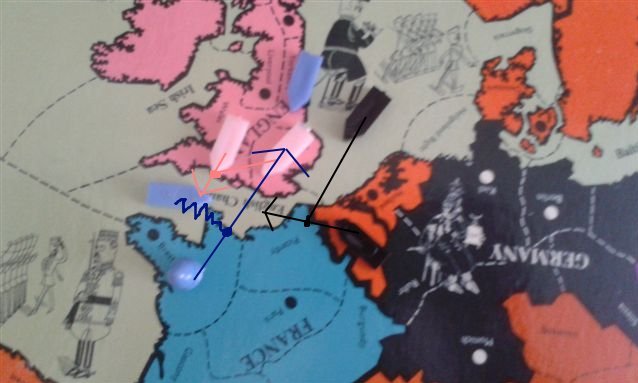
England: Fleet Wales – English Channel; Fleet London supports Wales – English Channel.
France: Army Brest – London; Fleet English Channel convoys Brest – London.
Germany: Fleet Belgium – English Channel; Fleet North Sea supports Belgium – English Channel.
This situation has been described before as Pandin's Paradox. Since we have a standoff in English Channel between England and Germany and no dislodgement occurs, the convoy is possible. However, despite the convoy’s success the attack still bounces. No support is cut, resulting in no change in board state.
But what happens if we add another piece?
England: Fleet Wales – English Channel; Fleet London supports Wales – English Channel.
France: Army Brest – London; Fleet English Channel convoys Brest – London; French Fleet Yorkshire supports Brest – London.
Germany: Fleet Belgium – English Channel; Fleet North Sea supports Belgium – English Channel.
(This example was used in Simon and Manus' article in the Zine Fall 1999 Retreat issue.)
Now the convoyed attack dislodges the English Fleet in London, so the support is cut. This means that the German attack on English Channel dislodges the French Fleet and disrupts the convoy. However, without the existence of a successful convoy, support from London would not be cut. This implies that the convoy is possible and thus introduces another paradox.
To solve this paradox and other kinds of paradoxes (see below) the rule above was changed into the following (Ed. Avalon Hill 1982):
If a convoyed army attacks a fleet which is supporting an action in or into a body of water, and that body contains a convoying fleet, that support is not cut not even if the supporting fleet is dislodged.
The resolution is then that the support from the English Fleet in London is still valid, even though it has been dislodged (and destroyed), and so there still is a standoff in English Channel.
This rule turned out to have some unforeseen consequences in cases where there was no paradox, so it was changed back to its original wording (Ed. Hasbro 2000).
During the discussion following Simon and Manus' article, it was suggested to solve the paradox by adding a new rule:
If a convoying fleet is attacked from two directions causing a standoff, but each of the attacks regarded separately would dislodge the fleet, then the fleet keeps its possession of the body of water, but the convoy does not take place.
This rule solves the paradox by resolving that the convoy doesn't take place. Personally, this rule appeals to me as I find it unrealistic that a convoy can be made through a body of water which two other fleets are fighting heavily for possession. Unfortunately, it is not a general solution of the paradox problem.
Let's look at another example:
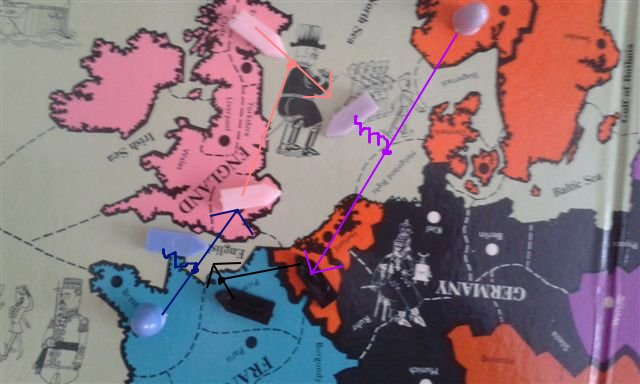
France: Army Brest – London; Fleet English Channel convoys Brest – London.
England: Fleet Edinburgh – North Sea; Fleet London supports Edinburgh – North Sea.
Russia: Army Norway – Belgium; Fleet North Sea convoys Norway – Belgium.
Germany: Fleet Picardy – English Channel; Fleet Belgium supports Picardy – English Channel.
Here you may say that the French attack on London cuts London’s support, causing the English attack on North Sea to bounce. The Russian attack on Belgium could also get through, cutting the support there as well. The German attack on English Channel would also bounce. Very well, but you may also argue that the German attack on English Channel would dislodge the French Fleet, making the convoy impossible. Thus the English attack on North Sea would succeed, dislodging the Russian Fleet and disrupting the convoy.
This exact paradox was the reason for the implementation of the Avalon Hill 1982 rule. The resolution was that both the convoying fleets are dislodged, thus preventing the convoys from taking place.
I don't prefer the Avalon Hill 1982 rule. It violates one of the basic premises of Diplomacy – one which states that a dislodged unit cannot offer support to another unit (it is busy running away). I don't believe that the cutting of support should be dependent on any external context. I find it ridiculous to have a rule stating that the support from a fleet to another fleet may be cut normally except when the supported fleet is attempting to convoy. It may solve the paradox, but the solution is artificial. Therefore, I fully agree with the return to the original wording (Ed. Hasbro 2000).
But we still have the paradox from Example 2.
Now (at last) I unveil my solution to this problem. I propose that the following rule be added:
If a convoying fleet is attacked, it is first determined if the convoy is possible without taking the convoyed attack into consideration. If there are several attacks of this kind, the possibility of these convoys are determined without any of these attacks. Afterwards, the possible convoyed attacks are added, and the results are determined as usual.
Note that a convoyed attack that is not attacked is immediately regarded as possible and included in the determination of the possible convoys.
Also note that the final determination of the results cannot change the possibility of the actual convoys, even if a convoying fleet is dislodged after making the convoy behind the army's back.
The justification for this rule is the same as stated above. Support is given before the cutting of support takes place. In other words, a convoyed attack consists of two phases: 1) Armies are convoyed across a body of water. 2) Coastal provinces are attacked. A lag may be assumed between these phases.
Now, what happens if you apply this rule to the examples above? In Example 1a, the French Fleet is dislodged from English Channel (same result), and in Example 1b the convoy is possible because of the standoff between England and Germany (again, same result). But what if the English Fleet is dislodged from London? One way of solving this is to append this text to the Hasbro 2000 rule: even if the fleet is dislodged. But as mentioned above, I would wish to avoid that if at all possible. I prefer having the support cut, and the result is then that the French Army goes to London, the English Fleet in London is destroyed, and the German Fleet goes to English Channel dislodging the French Fleet there – after the convoy has been made.
In Example 2 both convoying fleets are dislodged and the convoys don't take place – same solution as when using the Avalon Hill 1982 rule.
We now have to look at the rule in use on a case where there is no paradox.
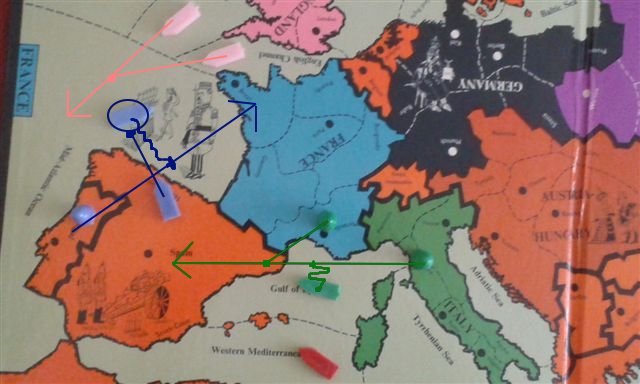
England: Fleet Irish Sea – Mid-Atlantic Ocean; Fleet English Channel supports Irish Sea – Mid-Atlantic Ocean.
France: Army Portugal – Brest; Fleet Mid-Atlantic Ocean convoys Portugal – Brest; Fleet Spain (nc) supports Mid-Atlantic Ocean.
Italy: Army Tuscany – Spain; Fleet Gulf of Lyon convoys Tuscany – Spain; Army Marseilles supports Tuscany – Spain.
The result using the Hasbro 2000 rule is that the support from the French Fleet in Spain is cut, and the Italian Army goes to Spain, dislodging the French Fleet. The attack on Mid-Atlantic Ocean also succeeds, so the English Fleet goes to Mid-Atlantic Ocean, dislodging the French Fleet. The convoyed attack on Brest would be unsuccessful.
Utilizing my suggestion would yield the same result.
However, a variation in results can be observed with the addition of the following order: Austrian Fleet in Western Mediterranean Sea – Gulf of Lyon. The results are unchanged using the Hasbro 2000 rule since the attack on the Gulf of Lyon is unimportant. Under my suggested revision, both convoys are under attack so their success should be determined first. A standoff would occur in Mid-Atlantic Ocean, which allows for the convoy. The convoy in Gulf of Lyon is, of course, also valid. The result is this: The French Army in Portugal goes to Brest. The French Fleet in Spain is dislodged, and the Italian Army from Tuscany goes to Spain. The English Fleet from Irish Sea goes to Mid-Atlantic Ocean dislodging the French Fleet there, after the convoy has been made.
The difference is that the French Army is convoyed to Brest before the support from Spain is cut. The attack on the convoy in Gulf of Lyon delays the attack on Spain by enough to allow the support for the convoy in Mid-Atlantic Ocean a chance to slip through.
Well, there you are! The suggested rule solves each of the convoy paradoxes, and the only price you pay is to allow a successfully convoying fleet to become dislodged from its field behind the back of the convoyed army. I feel that this solution is more realistic than that which is offered by Hasbro 2000, or another solution where the cutting of support depends on the behavior of the supported unit. Don't get me wrong, this solution is intended as a supplement to, not a replacement of, the Hasbro rule.

|
Torsten Bille (itbille@fasttvnet.dk) |
If you wish to e-mail feedback on this article to the author, and clicking
on the envelope above does not work for you, feel free to use the
Dear DP...
mail interface.