Towards a Machiavelli Hall of Fame

by Neil Barr

In 1988 I embarked upon a significant distraction from work on my thesis.... an attempt to create a Machiavelli Hall of Fame. The database for this project was initially based upon Nick Fitzpatrick’s Hall of Fame database. Thanks Nick. As extensive as Nick’s database is, it only includes details of games which completed by 1996. The appearance of any further games in the Hall of Fame database is unsure. Games which finished in 1997 and 1998 were added by gleaning information from game summaries or from the personal records of a number of current Machiavelli players.

As of April 1999, there are 57 completed (or abandoned) games in the database. Another 12 current games are included awaiting completion or a start. The database is at this stage incomplete. The minimum acceptable data set for each game is similar to that collected for the Hall of Fame. Where possible a full game summary would round things off. There are a number of games with only partial data. In particular, these games are missing the identities of some players or the outcomes for some powers. A small number of games may well be totally missing. A summary of the data status is shown in the table below. If a game is not listed in this table, I know nothing about it. Any past or present judge Machiavelli players can help by sending me details of games.

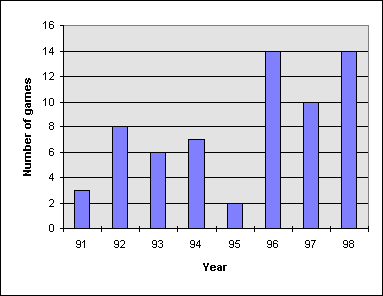
The first recorded games in the database started in 1991. From 92 to 97 the number of games each year was relatively stable. The small number of games recorded in 1995 may be in part a result of data shortages.

The "Balance of Power" scenario implemented on the judge is clearly anything but balanced. In the original boxed set the victory conditions are set at 15 centres. This represents less than half of the total 44 centres. The majority of judge games are played with 23 centre victory conditions which qualifies the games for Nick Fitzpatrick's Hall of Fame. A few games are currently playing towards 44 centre victory conditions. It will be interesting to see if the game enthusiasm lasts the distance. The initial evidence is less than heartening.

The next table show the performance of each power in the 23 centre games. HoF refers to the total "Hall of Fame" points achieved by each power. PSI refers to a skill index for each power calculated in a similar manner to the Diplomacy Skill Index. Results of powers eliminated from current unfinished games are included. Results of a small number of games which did not reach a conclusion due to judge failure are included where the result was well developed.

In 23 centre games Venice is clearly the superpower. With a 26% win rate, it has a greater chance of winning than being eliminated. Venice’s elimination rate is half the next nearest rates of France and Turkey. This reflects the difficulty of taking its island fortress and also its double variable income.

France is the second strongest power in the 23 centre game. But it is significantly weaker than Venice. If it weren’t for the plague prone nature of Marseille and Avignon, I believe France would be up there with Venice. Its single variable income is more than compensated for by the rich neutral cities on its borders. Turkey is close to par with France. Statistically there is probably no significant difference. Clearly both benefit from the corner status.

The next power group is the Papacy, Milan and Naples. The Papacy and Milan are clearly less secure than Naples with an elimination rate similar to that of Florence. Milan is an interesting performer. With three wins it matches all but Venice above it on the ladder. But currently there are no Milanese draws. Milan can win, but it has a high risk of elimination.

At the bottom of the table are the bridesmaids, Florence and Austria. Florence is potentially a strong power in the end game, if it can survive the initial years and eliminate the Papacy. The second variable income lifts it above the performance of Austria. With the highest elimination ratio of 73 per cent, Austria, suffers from its proximity to the super power Venice. Milan suffers a similar, though lesser danger in its proximity to France. My opinion is that Milan and Austria need to be firm allies to survive. But experience tells me that the proximity of Tyrolea and the city of Milan, and the prospect for Austria of the only simple conquest coming from Milan means this alliance often breaks down, and that Venice and France are the normal beneficiaries.

It is clear from the results of 15 centre games that this is a quite unbalanced scenario. France has won almost half of the games in the database. As could be expected, Venice achieved a reasonable share of wins. At the bottom end, Turkey’s position seems quite hopeless.

From these results it is quite possible to argue that Machiavelli is a flawed game due to the unbalanced nature of its results. A counter-argument to this position is that experienced players should realise the inherent strength of Venice in particular in the 23 centre game, and play accordingly. The strongest advocate of this position is Bruce Duewer, the undisputed "Prince of Machiavelli". Having won with each major power, he regularly argues that his easiest wins have been with Austria and Milan, because the opposition didn’t see them coming until too late. Being a regular player, I can support some of Bruce's argument. But given the regular core of players who feature in many games, it is still telling that Venice gets so many wins.

Bruce does not extend his arguments to the 15 centre game. These games are short, and some powers have a clearly superior access to neutral supply centres. I believe this scenario is fundamentally flawed and should be abandoned in favour of some other alternative. I believe there would be some value in implementing some other Machiavelli scenarios on the judge to achieve some more balanced outcomes. I see no reason to believe Machiavelli II will redress the problem. One option would be the other scenarios described in the original rule set. However, I suspect a number of these would be just as unbalanced. The Spanish preponderance would appear to fit this case. The weakness of the 15 centre game could be overcome by the "Expansion of the States" scenario with both a 19 centre and perhaps 13 centre victory condition. This would meet the need for a short game to act as a good introduction to Machiavelli rules and tactics.

Mach is not the most popular of the variants. The rules are a little more complicated than straight Diplomacy, and the judge implementation still has a few bugs. This shouldn’t put new players off. The game does have a committed band of devotees. Currently Bruce Duewer is the most experienced player with appearances in 26 games under his belt. To my knowledge there are approximately 20 current players normally active in multiple games. There is a steady influx of what I would call passing players, dabbling in the scenario before moving on. I am sure the more experienced Mach players would all suggest that there is no need to move on if one sticks to the 23 centre variant.

Note that these tables are based upon incomplete data. From my own experience I feel there are players I fear who have not shown up in these rankings. Any help in filling the gaps is welcomed.

In trying to build a measure of relative player performance, the small number of games in the database is a major limitation. A Machiavelli Skill Index cannot afford to use the homogeneity criteria of the DSI or the HoF. All game are included. There is no separation of differing press options, victory conditions or the variations to the optional rules of plague, famine, loans, assassination or adjacency. Within this limitation, I have attempted to create an analog of most of the current scoring systems used in the wider Diplomacy world. The exception is the DJPR system. The effort is not warranted given the small number of games.

A Machiavelli Hall of Fame

This is a score of cumulative performance since records commenced. Points are allocated to winners or drawers in each game according to the formula:

Points = (8-W)/W where W is # of winners (1) or people who shared in the draw.

In a standard game this gives 7.00 points for a win, 3.00 for a two-way draw, 1.67 for a 3 way and 1.00 for a four way draw. Points are awarded pro-rata according to the length of time in the game. Nick Fitzpatrick’s HoF only included mach games with 23 centres as the victory condition. However, many Mach games have a 15 centre victory condition. These games are included in the Mach HoF, adjusted by a pro-rata formula according to the victory conditions of the games. Thus a win in a 15 centre games is accorded approximately two thirds the value of a 23 centre game (4.56). Games with victory conditions greater than 23 centres are treated as 23 centre games. The following table shows players who have scored seven or more points.

The Hall of Fame does not indicate the relative success of a player. A win from 20 games scores the same as a win from one game. Neither does it reflect the relative difficulty of playing the differing powers in Machiavelli. And it does not fulfill one of the objects of a scoring system... to reward desirable behaviour. Other scoring systems attempt to fulfill some or all of these objectives.

• HoF Ratio. Simply the HoF score divided by the effective number of completed games participated in. To reduce the incentive to stop playing after an early win, the number of games is assumed to be at 8 if the player has in fact played fewer. Scores greater than .5 are included in the table below.

• YARS. A modification of HoF created by Bruce Duewer. Each player loses one point at the start of a game. Those sharing in the draw gain points according to the formula (9-W)/ W where W is the number of participants in the final result. Results are modified by pro-rata adjustments to reflect victory conditions and period of the game played by the player.

• Machiavelli Skill Index. This is plagiarised shamelessly from the Diplomacy Skill Index. In this version, winners receive 8 points. Participants in a draw receive 8/N points, where N is the number of draw participants. Survivors receive half a point for staying in the match. Eliminated players receive a quarter of a point. Abandoning players receive no points. These scores are amended by a ratio reflecting the relative success of each power in all games in the database. Thus, as the power performance stands, a Venetian win in a 23 centre game will gain 2.99 points, but an Austrian position in a three way draw is worth 5.13. These adjustments are crucial to for Machiavelli, and are a strong reason to favour this as a measure of Machiavelli performance. The current MSI awards for various powers are shown below.

  Table 7: Current reward for performance by each Machiavelli power in 23 centre games using the Machiavelli Skill Index (MSI)

  Power	MSI	Win	2 way	3 way	4 way	5 way	6 way	7 way	8 way	Surv	Elim
  Venice	2.68	2.99	1.49	1.00	0.75	0.60	0.50	0.43	0.37	0.19	0.09
  France	1.38	5.80	2.90	1.93	1.45	1.16	0.97	0.83	0.72	0.36	0.18
  Turkey	1.29	6.20	3.10	2.07	1.55	1.24	1.03	0.89	0.78	0.39	0.19
  Papacy	0.93	8.60	4.30	2.87	2.15	1.72	1.43	1.23	1.08	0.54	0.27
  Milan	0.88	9.09	4.55	3.03	2.27	1.82	1.52	1.30	1.14	0.57	0.28
  Naples	0.87	9.20	4.60	3.07	2.30	1.84	1.53	1.31	1.15	0.57	0.29
  Florence	0.76	10.53	5.26	3.51	2.63	2.11	1.75	1.50	1.32	0.66	0.33
  Austria	0.52	15.38	7.69	5.13	3.85	3.08	2.56	2.20	1.92	0.96	0.48

  In the MSI all scores are also adjusted to reflect victory conditions. Win and draw scores are adjusted to reflect period in the game. An index is created by dividing the total player score by the number of games played. If the effective number of games played is less than 8, then the total is divided by 8. Fifteen centre games are included with their own adjustment matrix. The result is an index of sorts.

  Table 8: Machiavelli Player Skill Index

  Player	MSI
  Bruce Duewer	3.83066
  Alex Simmons	1.47556
  Ken McArthur	1.34880
  Lynn Mercer	1.34750
  Steven Stuart	1.18494
  Ryan Wolfe	1.17834
  Ward Narhi	1.16633
  Don Kremer	1.14907
  Joe Urbank	1.13333
  Bill Kirby	1.04679
  John Rhodes	1.03604
  Andy Schwarz	0.93186
  Brian Barnes	0.91048
  Alan Thompson	0.86956
  Eric N. Coffey	0.83276
  Neil Barr	0.81498
  Charlie Eldred	0.64728
  Fernando Blesa	0.64628
  Chris Naughton	0.62396
  Gilles Ries	0.56213
  Alan Poulter	0.53483
  Alexander Finke	0.53446
  Dave Cebula	0.53309
  Eric Moore	0.50208
  Sean Pfeiffer	0.48309

So what can we make of all this? There is clearly only one Prince of Machiavelli, Bruce Duewer. No-one else has achieved a win with each power. To have achieved this with fewer than 21 effective games is a remarkable achievement. After Bruce there is a long tail in which the games have been shared around. And if each of his Mach games is included in the DJPR, his current leading position on that table will be consolidated. Those of us who have shared quite a few places in games with Bruce seem to be underperforming... I wonder why? All we can ask in return is a primer on Machiavelli strategy written by Bruce.

Neil Barr (nfbjgf@bendigo.net.au)

If you wish to e-mail feedback on this article to the author, click on the letter above. If that does not work, feel free to use the "Dear DP..." mail interface.