More recently, Manus dropped Simon a note, bringing up the topic again, with a proposal.
Simon examined Manus' proposed rule, and replied with a rule of his own which he had always had in mind to use should a paradoxical situation arise in a game he was running (it never did get used, as paradoxes are extremely uncommon situations). This rule also eliminated paradoxes, but in a different way and therefore resulting in a different outcome.
They now present these ideas for scrutiny by and for comment from the Diplomacy community.
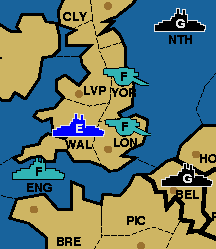
Here are the two proposed rules and the point/counter-point exchange between Simon and Manus. Consider the following situation (a slight modification on the traditional Pandin's paradox):
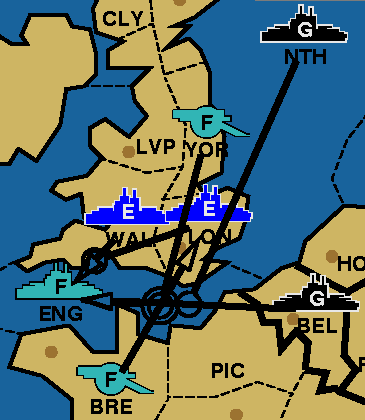
| Unit | Order | |||||
|---|---|---|---|---|---|---|---|
| English Fleet Wales English Fleet London | F Wal - ENG F Lon S F Wal - ENG French Army Brest | French Fleet English Channel French Army Yorkshire A Bre - ENG - Lon | F ENG C A Bre - Lon A Yor S A Bre - Lon German Fleet Belgium | German Fleet North Sea F Bel - ENG | F NTH S F Bel - ENG
| | |
If you adjudicate this situation according to the Diplomacy rules, you will find that it leads to a paradox. If the convoy to London fails, England and Germany have equally-well supported attacks on the English Channel, therefore there is a standoff. This, in turn, means that the Channel fleet is not dislodged, and therefore the convoy succeeds, cutting the support ordered by London. This causes Wal to lose support, eliminating the standoff in the Channel, allowing the German attack on the English Channel to succeed, dislodging the fleet there, and disrupting the convoy. This means that Brest does not attack London, reinstating the support given by London, causing a standoff, allowing the convoy to succeed, which cuts support... and so on and so on.
Why does this happen? Because there is an inconsistency in the Diplomacy rules that makes it impossible to adjudicate this situation without a paradox. Or, put slightly differently, there is no one single result that is consistent with the combination of rules on convoys, support, and support-cutting.
So how to eliminate the paradox? Simple. Add a rule that forbids paradoxes from happening. But you can't just add a rule that says "Paradoxes are forbidden" because such a rule would not tell you how the above (currently paradoxical) situation should be adjudicated. You need to come up with a rule that allows players to determine a single outcome for that situation.
Okay. Before we actually talk about specific paradox-eliminating rules, let's assume for a moment that we live in a world where such a rule exists. Okay? There is no paradox. Say it out loud. "There is no paradox." Good. The question is, since we have (in this imaginary world) a set of Diplomacy rules that does not result in a paradox for the above orders, what does the board look like after they are adjudicated? 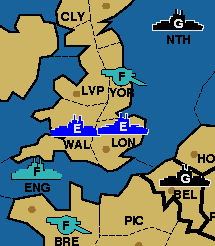Here are two possibilities:
| Resolution 1 | Resolution 2 | ||||||
|---|---|---|---|---|---|---|---|
|
| ||||||
English Fleet Wales
| English Fleet Wales
| English Fleet London French Army London | French Fleet English Channel French Army Yorkshire French Army Brest | French Fleet English Channel French Army Yorkshire German Fleet Belgium | German Fleet North Sea German Fleet Belgium | German Fleet North Sea Summary: The French convoy succeeds, dislodging
| and destroying the English fleet in London. Summary: No change in position
| |
Before discussing any actual rules, Simon and Manus want to get a gut reaction to the situation from readers. So please click on one of the buttons below to proceed to the rules and discussion. Note that you may not be 100% satisfied with either outcome, because this situation is one in which there fundamentally is no possible outcome that is completely consistent with all the Diplomacy rules. So we are not asking for absolute satisfaction... just which seems more right (or less wrong). If you absolutely just cannot make up your mind, you can click the third button. Regardless of how you answer now, you will be asked again after the discussion and will have the opportunity to change your mind.
|
Manus Hand (manus@manushand.com) |
|
|
Simon Szykman (simon@diplom.org) |
If you wish to e-mail feedback on this article to the authors, and clicking on an envelope above does not work for you, feel free to use the "Dear DP..." mail interface.
